题目内容
大学生李某投资在沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日采购进一种今年新上市的文具袋.9月份(9月1日至9月30日)进行30天的试销售,购进价格为20
元/个.销售结束后,得知日销售量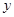 (个)与销售时间
(个)与销售时间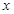 (天)之间有如下关系:
(天)之间有如下关系: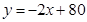 (
(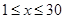 ,且
,且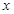 为整数);又知销售价格
为整数);又知销售价格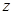 (元/个)与销售时间
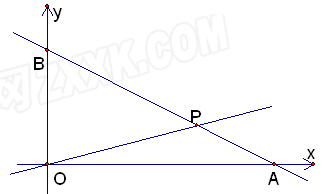
(元/个)与销售时间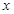 (天)之间的函数关系满足如图所示的函数图像.
(天)之间的函数关系满足如图所示的函数图像.
(1)求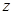 关于
关于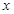 的函数关系式;
的函数关系式;
(2)求出在这30天(9月1日至9月30日)的试销中,日销售利润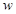 (元)与销售时间
(元)与销售时间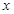 (天)之间的函数关系式;
(天)之间的函数关系式;
(3)“十一”黄金周期间,李某采用降低售价从而提高日销售量的销售策略.10月1日全天,销售价格比9月30日的销售价格降低 而日销售量就比9月30日提高了
而日销售量就比9月30日提高了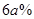 (其中
(其中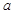 为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求
为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求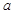 的值.
的值.
 (参考数据:
(参考数据: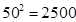 ,
,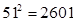 ,
, )
)
元/个.销售结束后,得知日销售量
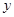 (个)与销售时间
(个)与销售时间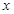 (天)之间有如下关系:
(天)之间有如下关系: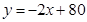 (
(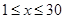 ,且
,且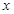 为整数);又知销售价格
为整数);又知销售价格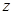 (元/个)与销售时间
(元/个)与销售时间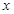 (天)之间的函数关系满足如图所示的函数图像.
(天)之间的函数关系满足如图所示的函数图像.(1)求
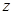 关于
关于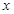 的函数关系式;
的函数关系式;(2)求出在这30天(9月1日至9月30日)的试销中,日销售利润
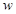 (元)与销售时间
(元)与销售时间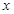 (天)之间的函数关系式;
(天)之间的函数关系式;(3)“十一”黄金周期间,李某采用降低售价从而提高日销售量的销售策略.10月1日全天,销售价格比9月30日的销售价格降低
 而日销售量就比9月30日提高了
而日销售量就比9月30日提高了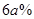 (其中
(其中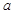 为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求
为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求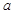 的值.
的值. (参考数据:
(参考数据: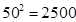 ,
,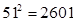 ,
, )
)25.(1)由图像知,当1≤x≤20时,设z=kx+b则有

当20<x≤30时z=45

(2)当1≤x≤20时,

=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)
=-50x+2000

(3)9月30日的价格为45元,日销售量为20个
9月份当1≤x≤20时日销售利润为
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元
综上9月份日销售利润最大为1225元.
由题意得45(1-a%)·20(1+6a%)-20×20(1+6a%)=1225-569
化简得18a2-700a+5200=0
a1=10,
答:a的值为10.

当20<x≤30时z=45

(2)当1≤x≤20时,

=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)
=-50x+2000

(3)9月30日的价格为45元,日销售量为20个
9月份当1≤x≤20时日销售利润为
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元
综上9月份日销售利润最大为1225元.
由题意得45(1-a%)·20(1+6a%)-20×20(1+6a%)=1225-569
化简得18a2-700a+5200=0
a1=10,

答:a的值为10.
分析:(1)根据图象得出销售价格z与销售时间x(天)的关系为一次函数关系进而求出即可;
(2)根据当1≤x≤20时,以及当20<x≤30时,表示出日销售利润,进而求出函数关系式即可;
(3)首先利用(2)中所求解析式,利用二次函数的最值求法以及一次函数的增减性,得出9月份日销售利润最大为1225元,再利用已知列出等式方程45(1-a%)?20(1+6a%)-20×20(1+6a%)=1225-569进而求出a的值即可.
解:(1)由图像知,当1≤x≤20时,设z=kx+b则有

当20<x≤30时z=45

(2)当1≤x≤20时,

=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)
=-50x+2000

(3)9月30日的价格为45元,日销售量为20个
9月份当1≤x≤20时日销售利润为
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元
综上9月份日销售利润最大为1225元.
由题意得45(1-a%)·20(1+6a%)-20×20(1+6a%)=1225-569
化简得18a2-700a+5200=0
a1=10,

答:a的值为10.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


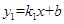 和反比例函数
和反比例函数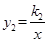 (
(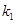 ?
?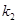 ≠0)的图像如图所示,若
≠0)的图像如图所示,若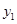 >
>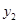 ,则
,则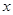 的取值范围是( ).
的取值范围是( ).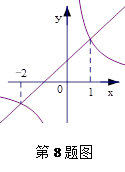
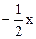 +1与x轴、y轴的交点
+1与x轴、y轴的交点
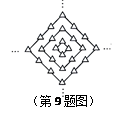
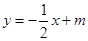 与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且
与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且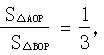 ,试求点P的坐标.
,试求点P的坐标.