Question

【题目】如图，一块四边形土地，其中，，，，，求这块土地的面积．

Answer 1

【答案】2400cm2

【解析】

延长CA、DB交于点P，利用含30度角的直角三角形在Rt△CDP中勾股定理可以求出PD，在Rt△PAB中可以求出PA，四边形的面积S四边形ACDB=S△CDP-S△ABP，就可以求得．

解：延长CA、DB交于点P

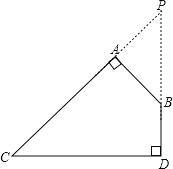
∵∠ABD=120°，AB⊥AC，BD⊥CD．
∴∠ACD=60°，∠ABP=60°，

∴∠CPD=30°，∠APB=30°，

∴CD=PC,AB=PB，

∵，，

∴PC=100cm,PB=60cm,

∴PD=cm,PA=cm,
∴S四边形ACDB=S△CDP-S△ABP
=×50×150-×30×90
=2400
答：这块土地的面积为2400cm2．