题目内容
记方程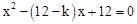 的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
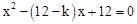 的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .
的两实数根为x1、x2,在平面直角坐标系中有三点A、B、C,它们的坐标分别为A (x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,则实数k的值为 .5或19.
试题分析:根据题意求得AB=1,然后利用根与系数的关系列出关于k的方程,通过解方程来求k的值:
∵A(x1,0),B(x2,0),C(0,12),若以此三点为顶点构成的三角形面积为6,
∴
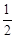 AB×12=6,解得AB=1,即
AB×12=6,解得AB=1,即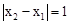 . ∴
. ∴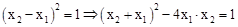 .
.∵方程
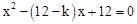 的两实数根为x1、x2,∴
的两实数根为x1、x2,∴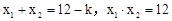 ,且
,且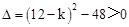 .
.∴
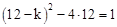 ,解得k=5或k=19.
,解得k=5或k=19.经检验,k=5和k=19都满足
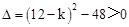 .
.∴k=5或k=19.

练习册系列答案
相关题目

 的图象的顶点坐标是( )
的图象的顶点坐标是( ) (m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程
(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程 的两实数根是
的两实数根是 的图像至少有三个公共点,则实数b的取值范围 .
的图像至少有三个公共点,则实数b的取值范围 .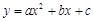 的图象如图所示,则下列结论中:①
的图象如图所示,则下列结论中:① ;②
;②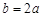 ;③
;③ ;④
;④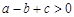 .正确的是 .
.正确的是 .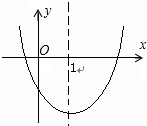
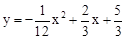 ,则铅球推出距离 米.
,则铅球推出距离 米.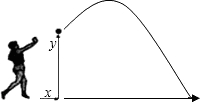
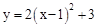 的图象的顶点坐标是( )
的图象的顶点坐标是( )