Question

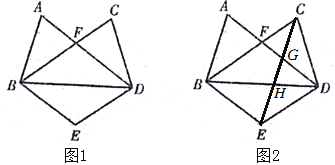
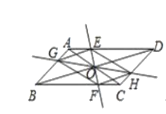
【题目】已知：如图，AB为⊙O的直径，C是BA延长线上一点，CP切⊙O于P，弦PD⊥AB于E，过点B作BQ⊥CP于Q，交⊙O于H．

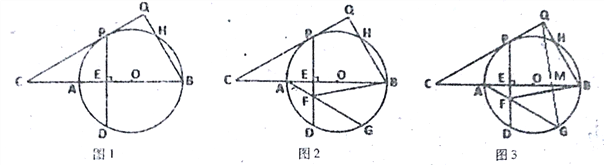
（1）如图1，求证：PQ=PE；

（2）如图2，G是圆上一点，∠GAB=30，连接AG交PD于F，连接BF，tan∠BFE=，求∠C的度数；

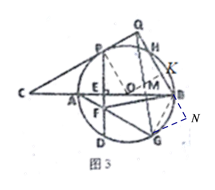
（3）如图3，在（2）的条件下，PD=6，连接QG交BC于点M，求QM的长．

Answer 1

【答案】（1）证明见解析（2）30°(3) QM=

【解析】试题分析：

（1）连接OP，PB，由已知易证∠OBP=∠OPB=∠QBP，从而可得BP平分∠OBQ，结合BQ⊥CP于点Q，PE⊥AB于点E即可由角平分线的性质得到PQ=PE；

（2）如下图2，连接OP，则由已知易得∠CPO=∠PEC=90°，由此可得∠C=∠OPE，设EF=x，则由∠GAB=30°，∠AEF=90°可得AE= ，在Rt△BEF中，由tan∠BFE=可得BE= ，从而可得AB= ，则OP=OA= ，结合AE= 可得OE= ，这样即可得到sin∠OPE=，由此可得∠OPE=30°，则∠C=30°；

（3）如下图3，连接BG，过点O作OK⊥HB于点K，结合BQ⊥CP，∠OPQ=90°，可得四边形POKQ为矩形．由此可得QK=PO，OK∥CQ从而可得∠KOB=∠C=30°；由已知易证PE=，在Rt△EPO中结合（2）可解得PO=6，由此可得OB=QK=6；在Rt△KOB中可解得KB=3，由此可得QB=9；在△ABG中由已知条件可得BG=6，∠ABG=60°；过点G作GN⊥QB交QB的延长线于点N，由∠ABG=∠CBQ=60°，可得∠GBN=60°，从而可得解得GN=，BN=3，由此可得QN=12，则在Rt△BGN中可解得QG=，由∠ABG=∠CBQ=60°可知△BQG中BM是角平分线，由此可得QM：GM=QB：GB=9：6由此即可求得QM的长了.

试题解析：

（1）如下图1，连接OP，PB，∵CP切⊙O于P，

∴OP⊥CP于点P，

又∵BQ⊥CP于点Q，

∴OP∥BQ，

∴∠OPB=∠QBP，

∵OP=OB，

∴∠OPB=∠OBP，

∴∠QBP=∠OBP，

又∵PE⊥AB于点E，

∴PQ=PE；

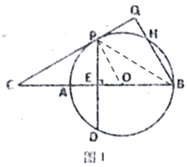
（2）如下图2，连接，∵CP切⊙O于P，

∴

∴

∵PD⊥AB

∴

∴

∴

在Rt中,∠GAB=30°

∴设EF=x，则

在Rt中,tan∠BFE=3

∴

∴

∴

∴

∴在RtPEO中,

∴30°；

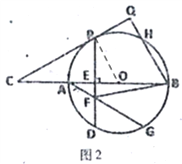
(3)如下图3，连接BG，过点O作于K，又BQ⊥CP，

∴，

∴四边形POKQ为矩形，

∴QK=PO,OK//CQ，

∴30°，

∵⊙O 中PD⊥AB于E ，PD=6 ，AB为⊙O的直径，

∴PE= PD= 3，

根据(2)得，在RtEPO中， ，

∴，

∴OB=QK=PO=6，

∴在Rt中， ，

∴，

∴QB=9，

在△ABG中，AB为⊙O的直径，

∴AGB=90°，

∵BAG=30°，

∴BG=6， ABG=60°，

过点G作GN⊥QB交QB的延长线于点N，则∠N=90°，∠GBN=180°-∠CBQ-∠ABG=60°，

∴BN=BQ·cos∠GBQ=3，GN=BQ·sin∠GBQ=，

∴QN=QB+BN=12，

∴在Rt△QGN中，QG=，

∵∠ABG=∠CBQ=60°，

∴BM是△BQG的角平分线，

∴QM：GM=QB：GB=9：6，

∴QM=.