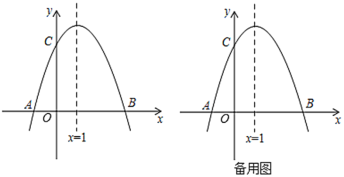
题目内容
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
【答案】(1)![]() ,
,![]() 点坐标为
点坐标为![]() ;(2)F
;(2)F![]() ;(3)
;(3)![]()
【解析】
(1)先求出点A,B的坐标,将A、B的坐标代入![]() 中,即可求解;
中,即可求解;
(2)确定直线BC的解析式为y=x+3,根据点E、F关于直线x=1对称,即可求解;
(3) 若![]() 与
与![]() 相似,则
相似,则![]() 或
或![]() ,即可求解;
,即可求解;
解:(1)∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,![]() ,∴
,∴![]() ,
,![]() .
.
代入![]() 中,得:
中,得:![]() ,解
,解![]() ,
,
∴抛物线的解析式为![]() .
.
∴![]() 点坐标为
点坐标为![]() ;
;
(2)设直线![]() 的解析式为
的解析式为![]() ,则有:
,则有:![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 、
、![]() 关于直线
关于直线![]() 对称,
对称,
又![]() 到对称轴的距离为1,∴
到对称轴的距离为1,∴![]() .
.
∴![]() 点的横坐标为2,将
点的横坐标为2,将![]() 代入
代入![]() 中,得:
中,得:![]() ,
,
∴F(2,1);
(3)![]() 秒时,
秒时,![]() .如图
.如图
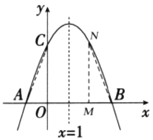
当![]() 时
时
![]()
![]()
∴![]() ,∴
,∴![]() ,
,
![]() .
.
①若![]() ,则
,则![]() ,即
,即![]()
![]() (舍去),或
(舍去),或![]() .
.
②若![]() ,则
,则![]() ,即
,即![]()
![]() (舍去),或
(舍去),或![]() (舍去)
(舍去)
∴![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目