题目内容
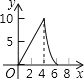
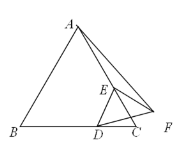
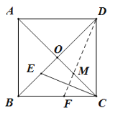
【题目】如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿DF直线折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM的长为________.
【答案】![]()
【解析】
连结EF.先证明△BEF是等腰直角三角形,求出BE=EF=CF=![]() ,根据△ODM∽△CDF,求出OM.
,根据△ODM∽△CDF,求出OM.
解:如图,连结EF.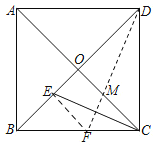
∵四边形ABCD是正方形,
∴AB=AD=BC=CD=2,
∠DCB=∠COD=∠BOC=90°,OD=OC,
∴BD=![]() ,
,
折叠性质可知,∠OEF=∠DCB=90°,∠EDF=∠CDF,
∴∠BEF=90°,
∴∠BFE=∠FBE=45°,
∴△BEF是等腰直角三角形,
∴BE=EF=CF=![]() ,
,
∵∠DCB=∠COD=90°,∠EDF=∠CDF,
∴△ODM∽△CDF,
∴![]() ,
,
即![]() ,
,
∴OM=![]() .
.
故答案为:![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
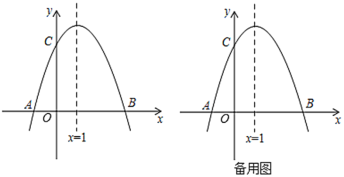
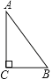
同步拓展阅读系列答案【题目】某班数学兴趣小组根据学习函数的经验,通过列表、描点、连线的方法对函数 y=![]() 的图象与性质进行了研究,研究过程如下,请补充完整.
的图象与性质进行了研究,研究过程如下,请补充完整.
(1)y 与 x 的几组对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | … |
y | … |
|
| 6 | 6 | m |
| … |
函数 y=![]() 的自变量 x 的取值范围是 ,m 的值为 ;
的自变量 x 的取值范围是 ,m 的值为 ;
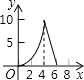
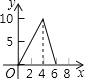
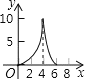
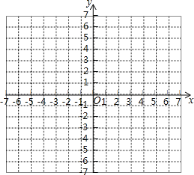
(2)在给出的平面直角坐标系中,描出以上表中各组对应值为坐标的点,画出函数 y=![]() 的大致图象,并写出该函数的两条性质;
的大致图象,并写出该函数的两条性质;
(3)在同一坐标系中画出函数 y1=![]() x 的图象,并根据图象直接写出当 y>y1 时,自变量 x 的取值范围.
x 的图象,并根据图象直接写出当 y>y1 时,自变量 x 的取值范围.
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查过程如下,请补充完整,
收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65
乙班:90,55,80,70,55,70,95,80,65,70
(1)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x人数班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=________;n=________.
(2)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 75 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=________,y=________.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀请估计乙班50名学生中身体素质为优秀的学生有________人.
【题目】某公司生产的商品的市场指导价为每件150元,公司的实际销售价格可以浮动![]() 个百分点[即销售价格
个百分点[即销售价格![]() ],经过市场调研发现,这种商品的日销售量
],经过市场调研发现,这种商品的日销售量![]() (件)与销售价格浮动的百分点
(件)与销售价格浮动的百分点![]() 之间的函数关系如下:
之间的函数关系如下:
浮动 | 0 | 1 | 2 | 3 | … |
销售量 | 24 | 22 | 20 | 18 | … |
若该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利10%.
个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产每件商品的成本为多少元?
(2)当实际销售价格定为多少元时,日销售利润为660元?[说明:日销售利润![]() (销售价格
(销售价格![]() 成本)
成本)![]() 日销售量];
日销售量];
(3)该公司决定每销售一件商品就捐赠![]() 元利润(
元利润(![]() )给希望工程,公司通过销售记录发现,当价格浮动的百分点大于
)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,直接写出
的增大而减小,直接写出![]() 的取值范围.
的取值范围.