题目内容
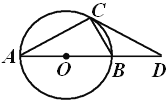
【题目】如图,以AB为直径的⊙O交∠BAD的平分线于点C,交AD于点F,过点C作CD⊥AD于D,交AB的延长线于点E.
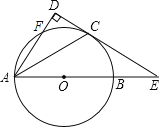
(1)求证:CD为⊙O的切线;
(2)若![]() =
=![]() ,求cos∠DAB的值.
,求cos∠DAB的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,如图,证明∠DAC=∠OCA得到AD∥OC,再利用平行线的性质得到OC⊥DE,然后根据切线的判定定理得到结论;
(2)作OH⊥AD于H,如图,则AH=HF,由四边形OCDH为矩形得到OH=CD,OC=DH,设CD=x,⊙O的半径为r,则AH=2x-r,OA=r,在Rt△OAH中利用勾股定理得到x2+(2x-r)2=r2,解得x=![]() r,然后利用余弦定义求解.
r,然后利用余弦定义求解.
(1)证明:连接OC,如图,
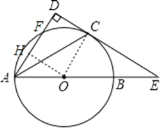
∵AC平分∠BAD,
∴∠DAC=∠EAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴CD为⊙O的切线;
(2)作OH⊥AD于H,如图,则AH=HF,
易得四边形OCDH为矩形,
∴OH=CD,OC=DH,
∵![]() =
=![]() ,
,
∴设CD=x,则AD=2x,
设⊙O的半径为r,
∴AH=2x﹣r,OA=r,
在Rt△OAH中,x2+(2x﹣r)2=r2,解得x=![]() r,
r,
∴AH=![]() r,
r,
在Rt△OAH中,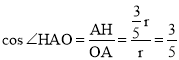 .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
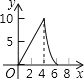
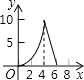
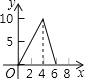
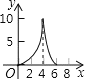
能考试全能100分系列答案【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.

小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
【题目】某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A.80≤m<85,B.85≤m<90,C.90≤m<95,D.95≤m≤100.另外给出了部分信息如下:
八年级10名学生的成绩:99,80,99,86,99,96,90,100,89,82.
九年级10名学生的成绩在C组的数据:94,90,94.
八、九年级抽取学生成绩统计表 | ||
年级 | 八年级 | 九年级 |
平均数 | 92 | 92 |
中位数 | 93 | b |
众数 | c | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)上面图表中的a= ,b= ,c= .
(2)扇形统计图中“D组”所对应的圆心角的度数为 .
(3)根据以上信息,你认为哪个年级的学生对“不忘初心,牢记使命”的内容掌握较好?说明理由.(一条即可)
(4)该校九年级共有840名学生参加了知识竞赛活动,估计九年级参加此次知识竞赛活动成绩为较好(90≤m<95)的学生有多少人?