МвДҝДЪИЭ
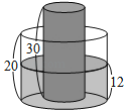
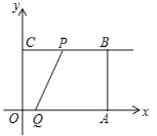
ЎҫМвДҝЎҝТСЦӘЈәИзНјЛщКҫЈ¬ФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЛДұЯРО
ЦРЈ¬ЛДұЯРО![]() КЗҫШРОЈ¬
КЗҫШРОЈ¬![]() Ј¬
Ј¬![]() Ј¬¶Ҝөг
Ј¬¶Ҝөг![]() ҙУөг
ҙУөг![]() іц·ўЈ¬СШЙдПЯ
іц·ўЈ¬СШЙдПЯ![]() ·ҪПтТФГҝГл2ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ»Н¬КұЈ¬¶Ҝөг
·ҪПтТФГҝГл2ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ»Н¬КұЈ¬¶Ҝөг![]() ҙУөг
ҙУөг![]() іц·ўЈ¬СШ
іц·ўЈ¬СШ![]() ЦбХэ°лЦб·ҪПтТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ¬Йиөг
ЦбХэ°лЦб·ҪПтТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ¬Йиөг![]() Ўўөг
Ўўөг![]() өДФЛ¶ҜКұјдОӘ
өДФЛ¶ҜКұјдОӘ![]()
ЈЁ1Ј©өұ![]() КұЈ¬Зуҫӯ№эөг
КұЈ¬Зуҫӯ№эөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ИэөгөДЕЧОпПЯөДҪвОцКҪЈ»
ИэөгөДЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©өұ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ3Ј©өұПЯ¶О![]() УлПЯ¶О
УлПЯ¶О![]() ПаҪ»УЪөг
ПаҪ»УЪөг![]() Ј¬ЗТ
Ј¬ЗТ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ4Ј©Б¬ҪУ![]() Ј¬өұөг
Ј¬өұөг![]() Ј¬
Ј¬![]() ФЪФЛ¶Ҝ№эіМЦРЈ¬јЗЎч
ФЪФЛ¶Ҝ№эіМЦРЈ¬јЗЎч![]() УлҫШРО
УлҫШРО![]() ЦШөюІҝ·ЦөДГж»эОӘ
ЦШөюІҝ·ЦөДГж»эОӘ![]() Ј¬Зу
Ј¬Зу![]() Ул
Ул![]() өДәҜКэ№ШПөКҪ
өДәҜКэ№ШПөКҪ
Ўҫҙр°ёЎҝЈЁ1Ј©y=©Ғ![]() x2+3xЈ»ЈЁ2Ј©
x2+3xЈ»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©tОӘ3sЈ»ЈЁ4Ј©S=
Ј»ЈЁ3Ј©tОӘ3sЈ»ЈЁ4Ј©S=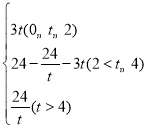
ЎҫҪвОцЎҝ
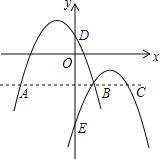
ЈЁ1Ј©ҝЙЗуөГPөгЧшұкЈ¬УЙOЎўPЎўAөДЧшұкЈ¬АыУГҙэ¶ЁПөКэ·ЁҝЙЗуөГЕЧОпПЯҪвОцКҪЈ»
ЈЁ2Ј©өұtЈҪ2sКұЈ¬ҝЙЦӘPУлөгBЦШәПЈ¬ФЪRtЎчABQЦРҝЙЗуөГtanЎПQPAөДЦөЈ»
ЈЁ3Ј©УГtҝЙұнКҫіцBPәНAQөДіӨЈ¬УЙЎчPBMЎЧЎчQAMҝЙөГөҪ№ШУЪtөД·ҪіМЈ¬ҝЙЗуөГtөДЦөЈ»
ЈЁ4Ј©өұөгQФЪПЯ¶ОOAЙПКұЈ¬SЈҪSЎчCPQЈ»өұөгQФЪПЯ¶ОOAЙПЈ¬ЗТөгPФЪПЯ¶ОCBөДСУіӨПЯЙПКұЈ¬УЙПаЛЖИэҪЗРОөДРФЦКҝЙУГtұнКҫіцAMөДіӨЈ¬УЙSЈҪSЛДұЯРОBCQMЈҪSҫШРОOABCSЎчCOQSЎчAMQЈ¬ҝЙЗуөГSУлtөД№ШПөКҪЈ»өұөгQФЪOAөДСУіӨПЯЙПКұЈ¬ЙиCQҪ»ABУЪөгMЈ¬АыУГЎчAQMЎЧЎчBCMҝЙУГtұнКҫіцAMЈ¬ҙУ¶шҝЙұнКҫіцBMЈ¬SЈҪSЎчCBMЈ¬ҝЙЗуөГҙр°ёЈ®
ҪвЈәЈЁ1Ј©өұt=1sКұЈ¬ФтCP=2Ј¬
ЎЯOC=3Ј¬ЛДұЯРОOABCКЗҫШРОЈ¬
ЎаPЈЁ2Ј¬3Ј©Ј¬ЗТAЈЁ4Ј¬0Ј©Ј¬
ЎЯЕЧОпПЯ№эФӯөгOЈ¬
ЎаҝЙЙиЕЧОпПЯҪвОцКҪОӘy=ax2+bxЈ¬
Ўа![]() Ј¬ҪвөГ
Ј¬ҪвөГ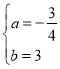 Ј¬
Ј¬
Ўа№эOЎўPЎўAИэөгөДЕЧОпПЯөДҪвОцКҪОӘy=©Ғ![]() x2+3xЈ»
x2+3xЈ»
ЈЁ2Ј©өұt=2sКұЈ¬ФтCP=2ЎБ2=4=BCЈ¬јҙөгPУлөгBЦШәПЈ¬OQ=2Ј¬ИзНј1Ј¬
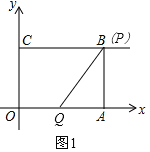
ЎаAQ=OA©ҒOQ=4©Ғ2=2Ј¬ЗТAP=OC=3Ј¬
ЎаtanЎПQPA=![]() =
=![]() Ј»
Ј»
ЈЁ3Ј©өұПЯ¶ОPQУлПЯ¶ОABПаҪ»УЪөгMЈ¬ФтҝЙЦӘөгQФЪПЯ¶ОOAЙПЈ¬өгPФЪПЯ¶ОCBөДСУіӨПЯЙПЈ¬ИзНј2Ј¬
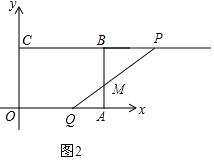
ФтCP=2tЈ¬OQ=tЈ¬
ЎаBP=PC©ҒCB=2t©Ғ4Ј¬AQ=OA©ҒOQ=4©ҒtЈ¬
ЎЯPCЎОOAЈ¬
ЎаЎчPBMЎЧЎчQAMЈ¬
Ўа![]() Ј¬ЗТBM=2AMЈ¬
Ј¬ЗТBM=2AMЈ¬
Ўа![]() =2Ј¬ҪвөГt=3Ј¬
=2Ј¬ҪвөГt=3Ј¬
ЎаөұПЯ¶ОPQУлПЯ¶ОABПаҪ»УЪөгMЈ¬ЗТBM=2AMКұЈ¬tОӘ3sЈ»
ЈЁ4Ј©өұ0ЎЬtЎЬ2КұЈ¬ИзНј3Ј¬

УЙМвТвҝЙЦӘCP=2tЈ¬
ЎаS=SЎчPCQ=![]() ЎБ2tЎБ3=3tЈ»
ЎБ2tЎБ3=3tЈ»
өұ2ЈјtЎЬ4КұЈ¬ЙиPQҪ»ABУЪөгMЈ¬ИзНј4Ј¬
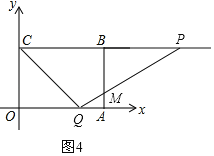
УЙМвТвҝЙЦӘPC=2tЈ¬OQ=tЈ¬ФтBP=2t©Ғ4Ј¬AQ=4©ҒtЈ¬
Н¬ЈЁ3Ј©ҝЙөГ![]() =
=![]() Ј¬
Ј¬
ЎаBM=![]() AMЈ¬
AMЈ¬
Ўа3©ҒAM=![]() AMЈ¬ҪвөГAM=
AMЈ¬ҪвөГAM=![]() Ј¬
Ј¬
ЎаS=SЛДұЯРОBCQM=SҫШРОOABC©ҒSЎчCOQ©ҒSЎчAMQ=3ЎБ4©Ғ![]() ЎБtЎБ3©Ғ
ЎБtЎБ3©Ғ![]() ЎБЈЁ4©ҒtЈ©ЎБ
ЎБЈЁ4©ҒtЈ©ЎБ![]() =24©Ғ
=24©Ғ![]() ©Ғ3tЈ»
©Ғ3tЈ»
өұtЈҫ4КұЈ¬ЙиCQУлABҪ»УЪөгMЈ¬ИзНј5Ј¬
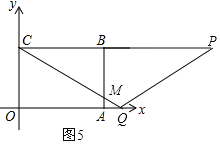
УЙМвТвҝЙЦӘOQ=tЈ¬AQ=t©Ғ4Ј¬
ЎЯABЎОOCЈ¬
Ўа![]() Ј¬јҙ
Ј¬јҙ![]() =
=![]() Ј¬ҪвөГAM=
Ј¬ҪвөГAM=![]() Ј¬
Ј¬
ЎаBM=3©Ғ![]() Ј¬
Ј¬
ЎаS=SЎчBCM=![]() ЎБ4ЎБ
ЎБ4ЎБ![]() Ј»
Ј»
ЧЫЙПҝЙЦӘS=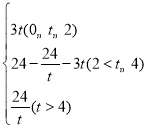 Ј®
Ј®

 ¶б№ЪҪрҫнИ«ДЬБ·ҝјПөБРҙр°ё
¶б№ЪҪрҫнИ«ДЬБ·ҝјПөБРҙр°ё