题目内容
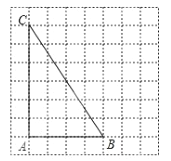
【题目】如图，是一圆锥的左视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小为（ ）
A.90°
B.120°
C.135°
D.150°
【答案】B
【解析】解：∵圆锥的底面半径为3，
∴圆锥的底面周长为6π，
∵圆锥的高是6 
，
∴圆锥的母线长为 
=9，
设扇形的圆心角为n°，
∴ 
=6π，
解得n=120．
答：圆锥的侧面展开图中扇形的圆心角为120°．
所以答案是：B．
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握弧长计算公式(若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的)的相关知识才是答题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
【题目】某中学为了科学建设“学生健康成长工程”，随机抽取了部分学生家庭对其家长进行了主题“周末孩子在家您关心了吗？”的调查问卷，将收回的调查问卷进行了分析整理，得到了如下的样本统计图表和扇形统计图：
代号 | 情况分类 | 家庭数 |
A | 带孩子玩且关心其作业完成情况 | 8 |
B | 只关心其作业完成情况 | m |
C | 只带孩子玩 | 4 |
D | 既不带孩子玩也不关心其作业完成情况 | n |
（1）求m，n的值；
（2）该校学生家庭总数为500，学校决定按比例在B、C、D类家庭中抽取家长组成培训班，其比例为B类20%，C、D类各取60%，请你估计该培训班的家庭数；
（3）若在C类家庭中只有一个是城镇家庭，其余是农村家庭，请用列举法求出C类中随机抽出2个家庭进行深度家访，其中有一个是城镇家庭的概率．
