Question

【题目】如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A（﹣1，0）、B（3，0），与y轴负半轴交于点C．

（1）若△ABD为等腰直角三角形，求此时抛物线的解析式；
（2）a为何值时△ABC为等腰三角形？
（3）在（1）的条件下，抛物线与直线y= x﹣4交于M、N两点（点M在点N的左侧），动点P从M点出发，先到达抛物线的对称轴上的某点E，再到达x轴上的某点F，最后运动到点N，若使点P运动的总路径最短，求点P运动的总路径的长．

Answer 1

【答案】
（1）

解：如图1，

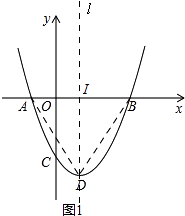
∵△ABD是等腰直角三角形，

∴过点D作直线l∥y轴，直线l与x轴交于点I．

∴AI=ID=IB= AB=2，

∴D（1，﹣2），

∴设y=a（x+1）（x﹣3）=ax2﹣2ax﹣3a，

∴a﹣2a﹣3a=﹣2，

∴a= ，

∴y= x2﹣x﹣

（2）

解：∵△ABC为等腰三角形，

∴①AB=BC=4，

∴OC= = ，

∴﹣3a=﹣ ，

∴a= ，

②AB=AC=4，

∴OC= = ，

∴C（0，﹣ ），

∴﹣3a=﹣ ，

∴a=

（3）

解：如图2，

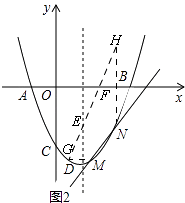
∵抛物线与直线y= x﹣4交于M、N两点，

∴ ，

∴ ， ，

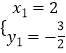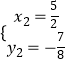∴M（2，﹣ ），N（ ，﹣ ）．

作点M关于对称轴l的对称点G，

点N关于x轴的对称点H，

连接GH交l于E，x轴于F，

∴EM=EH，FN=FH

∴点P运动的总路径为GH，

∵G（0，﹣ ），H（ ， ），

∴GH=

【解析】（1）由△ABD是等腰直角三角形确定出D（1，﹣2），用待定系数法确定出函数关系式；（2）由△ABC为等腰三角形，利用勾股定理求出a即可；（3）由于抛物线与直线y= x﹣4交于M、N两点，先求出M，N的坐标，利用对称性求出点G，H的坐标即可．
【考点精析】认真审题，首先需要了解二次函数的图象(二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点)，还要掌握二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)的相关知识才是答题的关键．