题目内容
【题目】如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( ) 
A.4﹣π
B.4﹣2π
C.8+π
D.8﹣2π
【答案】A
【解析】解: 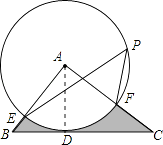
△ABC的面积是: ![]() BCAD=
BCAD= ![]() ×4×2=4,
×4×2=4,
∠A=2∠EPF=90°.
则扇形EAF的面积是: ![]() =π.
=π.
故阴影部分的面积=△ABC的面积﹣扇形EAF的面积=4﹣π.
故选A.
【考点精析】掌握切线的性质定理和扇形面积计算公式是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
相关题目
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正常字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= , n= , 并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数. 







