Question

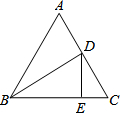
如图，已知△ABC是等边三角形，BD是中线，延长BC到E，使CE=CD，不添加辅助线，请你探究△BDE与△DCE中的边、角、面积之间的数量关系，并选择两种写出你的结论：______，______．

Answer 1

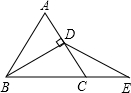
∵△ABC是等边三角形，BD是中线
∴∠DBC=

1

2

∠ABC=30°，CD=

1

2

AC=

1

2

BC，∠BDC=90°，∠C=60°
∴∠ACE=180°-60°=120°
∵CE=CD
∴BE=BC+CE=3CE，∠E=∠CDE=

180°-120°

2

=30°=∠DBC
∴△CED∽△EDB，∠ECD=∠BDE
∵tan∠BCD=BD：CD=tan60°=

3

∴S_△BDE：S_△ECD=BD²：CD²=3
即：S_△BDE=3S_△ECD．