题目内容
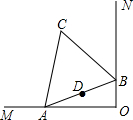
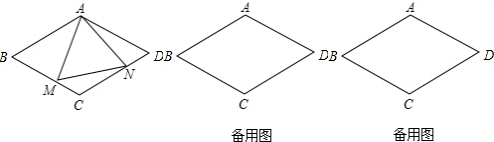
已知:如图,四边形ABCD中,AB=BC=CD=DA=a,∠BAD=120°,M为BC上的点(M不与B、C重合),若△AMN有一角等于60°.
(1)当M为BC中点时,则△ABM的面积为______(结果用含a的式子表示);
(2)求证:△AMN为等边三角形;
(3)设△AMN的面积为S,求出S的取值范围(结果用含a的式子表示).
(1)当M为BC中点时,则△ABM的面积为______(结果用含a的式子表示);
(2)求证:△AMN为等边三角形;
(3)设△AMN的面积为S,求出S的取值范围(结果用含a的式子表示).

如图,
在四边形ABCD中,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形,
又∵∠BAD=120°,
∴∠BCD=120°,∠B=∠D=60°,
连AC则,∠BAC=∠DAC=60°,∠BCA=∠DCA=60°,AC=AB=AD.
(1)如上图,
当M为BC中点时,
∴AM⊥BC,
∴S△ABM=
S△ABC=
×
a×
a=
a2;
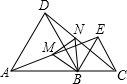
(2)①、如图1:

如果∠MAN=60°,
则∠MAC+∠CAN=60°,∵∠BAC=60°,
∴∠BAM+∠MAC=60°,
∴∠BAM=∠CAN,
AB=AC,
∠B=∠ACN=60°,
∴△ABM≌△ACN,
∴AM=AN,
∴△AMN是正三角形;
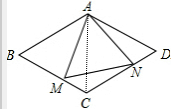
②、如图2:
如果∠AMN=60°,
则∠AMC=∠B+∠1=60°+∠1,
∵∠AMC=60°+∠2,
∴∠1=∠2,
又∵∠AMN=∠ACN=60°,
∴A、M、C、N四点共圆,
∴∠2=∠3,
∴∠1=∠3,
AB=AC,
∠B=∠ACN=60°,
∴△ABM≌△ACN,
∴AM=AN,
∴△AMN是正三角形;
③、如图3,
如果∠ANM=60°,
则∠ANC=∠D+∠6=60°+∠6,
∵∠ANC=60°+∠5,
∴∠5=∠6,
又∵∠ANM=∠ACM=60°,
∴A、N、C、M四点共圆,
∴∠4=∠5,
∴∠4=∠6,
AC=AD,
∠ACM=∠D=60°,
∴△AMC≌△AND,
∴AMAN,
∴△AMN是正三角形;
(3)最大S△ABM=
S菱形ABCD=
a×
a=
a2,
最小S△ABM=
×
a×
a=
a2,
∴
a2≤S△ABM≤
a2.

在四边形ABCD中,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形,
又∵∠BAD=120°,
∴∠BCD=120°,∠B=∠D=60°,
连AC则,∠BAC=∠DAC=60°,∠BCA=∠DCA=60°,AC=AB=AD.
(1)如上图,
当M为BC中点时,
∴AM⊥BC,
∴S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
(2)①、如图1:

如果∠MAN=60°,
则∠MAC+∠CAN=60°,∵∠BAC=60°,
∴∠BAM+∠MAC=60°,
∴∠BAM=∠CAN,
AB=AC,
∠B=∠ACN=60°,
∴△ABM≌△ACN,
∴AM=AN,
∴△AMN是正三角形;
②、如图2:
如果∠AMN=60°,
则∠AMC=∠B+∠1=60°+∠1,
∵∠AMC=60°+∠2,
∴∠1=∠2,
又∵∠AMN=∠ACN=60°,
∴A、M、C、N四点共圆,
∴∠2=∠3,
∴∠1=∠3,
AB=AC,
∠B=∠ACN=60°,
∴△ABM≌△ACN,
∴AM=AN,
∴△AMN是正三角形;
③、如图3,
如果∠ANM=60°,
则∠ANC=∠D+∠6=60°+∠6,
∵∠ANC=60°+∠5,
∴∠5=∠6,
又∵∠ANM=∠ACM=60°,
∴A、N、C、M四点共圆,
∴∠4=∠5,
∴∠4=∠6,
AC=AD,
∠ACM=∠D=60°,
∴△AMC≌△AND,
∴AMAN,
∴△AMN是正三角形;
(3)最大S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
最小S△ABM=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 4 |
3
| ||
| 16 |
∴
3
| ||
| 16 |
| ||
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目