��Ŀ����
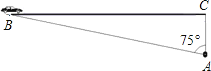
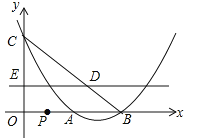
����Ŀ��������![]() ��x�ύ��A��B���㣨OA��OB������y�ύ�ڵ�C��
��x�ύ��A��B���㣨OA��OB������y�ύ�ڵ�C��
��1�����A��B��C�����ꣻ
��2����P�ӵ�O��������ÿ��2����λ���ȵ��ٶ����B�˶���ͬʱ��EҲ�ӵ�O��������ÿ��1����λ���ȵ��ٶ����C�˶������P���˶�ʱ��Ϊt�루0��t��2����
������E��x���ƽ���ߣ���BC�ཻ�ڵ�D����ͼ��ʾ������tΪ��ֵʱ��![]() ��ֵ��С����������Сֵ��д����ʱ��E��P�����ꣻ
��ֵ��С����������Сֵ��д����ʱ��E��P�����ꣻ
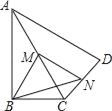
�����������������£������ߵĶԳ������Ƿ���ڵ�F��ʹ��EFPΪֱ�������Σ������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A��2��0����B��4��0����C��0��2������2����t=1ʱ��![]() ����Сֵ1����ʱOP=2��OE=1����E��0��1����P��2��0������F��3��2������3��7����
����Сֵ1����ʱOP=2��OE=1����E��0��1����P��2��0������F��3��2������3��7����
��������
���⣨1���������ߵĽ���ʽ�У���y=0����x=0���ⷽ�̼��ɵõ������
��2����������ã�OP=2t��OE=t��ͨ����CDE�ס�CBO�õ�![]() ����
����![]() �����
�����![]() ����Сֵ1��������ý����
����Сֵ1��������ý����
�����ڣ���������ߵĶԳƷ���Ϊx=3����F��3��m��������EFPΪֱ��������ʱ��������EPF=90��ʱ��������EFP=90��ʱ��������PEF=90��ʱ�����ݹ��ɶ����з��̼�����ý����
�����������1���������ߵĽ���ʽ�У���y=0����![]() ����ã�
����ã�![]() ��
��![]() ����OA��OB����A��2��0����B��4��0�����������ߵĽ���ʽ�У���x=0����y=2����C��0��2����
����OA��OB����A��2��0����B��4��0�����������ߵĽ���ʽ�У���x=0����y=2����C��0��2����
��2����������ã�OP=2t��OE=t����DE��OB�����CDE�ס�CBO����![]() ����
����![]() ����DE=4��2t��
����DE=4��2t��
��![]() =
=![]() =
=![]() =
=![]() ����0��t��2��
����0��t��2��![]() ʼ��Ϊ��������t=1ʱ��
ʼ��Ϊ��������t=1ʱ��![]() �����ֵ1����t=1ʱ��
�����ֵ1����t=1ʱ��![]() ����Сֵ1����t=1ʱ��
����Сֵ1����t=1ʱ��![]() ����Сֵ1����ʱOP=2��OE=1����E��0��1����P��2��0����
����Сֵ1����ʱOP=2��OE=1����E��0��1����P��2��0����
�����ڣ���������![]() �ĶԳ��᷽��Ϊx=3����F��3��m������
�ĶԳ��᷽��Ϊx=3����F��3��m������![]() ��
��![]() =
=![]() ��
��![]() =
=![]() ��
��
����EFPΪֱ��������ʱ��
������EPF=90��ʱ��![]() ����
����![]() ����ã�m=2��
����ã�m=2��
������EFP=90��ʱ��![]() ����
����![]() ����ã�m=0��m=1������������ȥ��������EFP=90��ʱ��������������ڣ�
����ã�m=0��m=1������������ȥ��������EFP=90��ʱ��������������ڣ�
������PEF=90��ʱ��![]() ����
����![]() ����ã�m=7��
����ã�m=7��
����������F��3��2������3��7����

����Ŀ��Ϊ������̬��������ֹˮ����ʧ��ij��ƻ��ڽ���������ֲ���������ּס��������ֳ�����ͬ�İ�������ɹ�ѡ����������۷������£�
���ֳ� | ���ֳ� | ||
���������� | ���۵��� | ���������� | ���۵��� |
������1000��ʱ | 4Ԫ/�� | ������2000��ʱ | 4Ԫ/�� |
����1000�õIJ��� | 3.8Ԫ/�� | ����2000�õIJ��� | 3.6Ԫ/�� |
�蹺���������x�ã��������ֳ�����������÷ֱ�Ϊy����Ԫ����y����Ԫ����
��1���ô���Ҫ����1500�ð������磬�����ڼ��ֳ������������Ϊ�� ��Ԫ�����������ֳ������������Ϊ�� ��Ԫ��
��2���ֱ����y����y����x֮��ĺ�����ϵʽ��
��3��������Ǹô�ĸ����ˣ�Ӧ��ѡ���ļ��ֳ�����������㣬Ϊʲô��
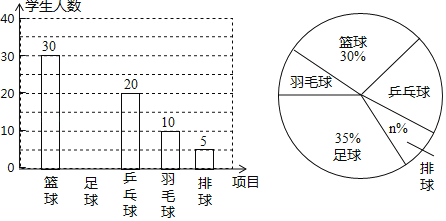
����Ŀ��Ϊ�����ѧ�����������ʣ�ij�༶������չ������Ҫ��ÿ��ѧ��������������������ƹ������ë����ѡ��һ��μ�ѵ����ֻѡ��һ�������ѧ���ı�������Ƴ�����ͳ�Ʊ���
��Ŀ | ���� | ���� | ���� | ƹ���� | ��ë�� |
�������� | 12 | 8 | 4 | a | 10 |
ռ�������İٷֱ� | 24% | b |
��1���ð�ѧ����������Ϊ�� ���ˣ�
��2���ɱ��е����ݿ�֪��a���� ����b���� ����
��3�������μ�����ѵ�����ĸ���Ϊ���У��ֱ��ΪA��B����Ů���ֱ��ΪC��D������Ҫ�������4����ѡ2�˲μ�ѧУ��֯��У��ѵ���������б�����״ͼ�ķ�������պ�ѡ��һ��һŮ�ĸ��ʣ�