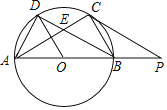
ЬтФПФкШн
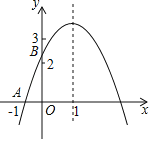
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНx2ЃЋbxЃЋcгыxжсНЛгкAЃЈЃ1ЃЌ0ЃЉЃЌгыyжсНЛгкCЃЈ0ЃЌЃ2ЃЉЃЛжБЯп![]() ОЙ§ЕуAЧвгыХзЮяЯпНЛгкСэвЛЕуB
ОЙ§ЕуAЧвгыХзЮяЯпНЛгкСэвЛЕуB![]() ЃЎ
ЃЎ
ЃЈ1ЃЉжБНгаДГіХзЮяЯпЕФНтЮіЪН ЃЛ
ЃЈ2ЃЉШчЭМЃЈ1ЃЉЃЌЕуMЪЧХзЮяЯпЩЯAЃЌBСНЕуМфЕФШЮвЛЖЏЕуЃЌMNЁЭABгкЕуNЃЌЪдЧѓГіMNЕФзюДѓжЕ ЃЌВЂЧѓГіMNзюДѓЪБЕуMЕФзјБъЃЛ
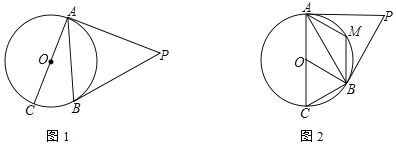
ЃЈ3ЃЉШчЭМЃЈ2ЃЉЃЌСЌНгACЃЌвбжЊЕуPЕФзјБъЮЊЃЈ2ЃЌ1ЃЉЃЌЕуQЮЊЖдГЦжсзѓВрЕФХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЙ§ЕуQзїQFЁЭxжсгкЕуFЃЌЪЧЗёДцдкетбљЕФЕуQЃЌЪЙЕУЁЯFQPЃНЁЯCAOЃЎШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
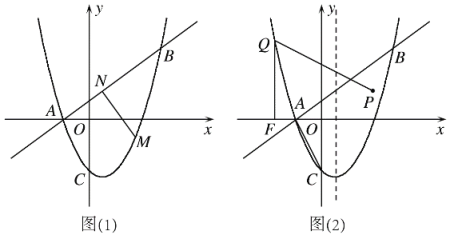
ЁОД№АИЁПЃЈ1ЃЉyЃНx2ЃxЃ2 ЃЛЃЈ2ЃЉ![]() ЃЛMЃЈ
ЃЛMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкЃЛЃЈ
ЃЉЃЛЃЈ3ЃЉДцдкЃЛЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉАбAЃЌCСНЕузјБъДњШыyЃНx2ЃЋbxЃЋcЧѓГіbЃЌcЕФжЕМДПЩЃЛ
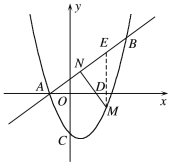
ЃЈ2ЃЉЙ§ЕуMзїMEЁЭxжсгкЕуDЃЌНЛABгкЕуEЃЌЩшM(mЃЌm2ЃmЃ2)ЃЌдђE(mЃЌ![]() mЃЋ
mЃЋ![]() ),ПЩЧѓГіMEЃНЃm2ЃЋ
),ПЩЧѓГіMEЃНЃm2ЃЋ![]() mЃЋ
mЃЋ![]() ЃЌжЄУїЁїAEDЁзЁїMENЕУMNЃНЃ
ЃЌжЄУїЁїAEDЁзЁїMENЕУMNЃНЃ![]() m2ЃЋ
m2ЃЋ![]() mЃЋ
mЃЋ![]() ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪПЩЕУНсТлЃЛ
ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪПЩЕУНсТлЃЛ
ЃЈ3ЃЉЕуQгаСНИіЮЛжУЃЌЪЙЕУЁЯFQPЃНЁЯCAOЃЌЗжБ№ЧѓГіДЫЪБPQЕФНтЮіЪНЃЌгыХзЮяЯпЗНГЬСЊСЂЗНГЬзщЃЌЧѓГіЗНГЬзщЕФНтМДЮЊQЕуЕФзјБъ.
НтЃКЃЈ1ЃЉНЋAЃЈ-1,0ЃЉЃЌCЃЈ0ЃЌ-2ЃЉДњШыНтЮіжаЕУ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2ЃxЃ2ЃЌ
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуMзїMEЁЭxжсгкЕуDЃЌНЛABгкЕуE.
ЩшM(mЃЌm2ЃmЃ2) (Ѓ1ЁмmЁм![]() )ЃЌ
)ЃЌ
дђE(mЃЌ![]() mЃЋ
mЃЋ![]() ),
),
MEЃН(![]() mЃЋ
mЃЋ![]() )Ѓ(m2ЃmЃ2)ЃНЃm2ЃЋ
)Ѓ(m2ЃmЃ2)ЃНЃm2ЃЋ![]() mЃЋ
mЃЋ![]() .
.
дкЁїAEDгыЁїMENжаЃЌЁЯAEDЃНЁЯMENЃЌЁЯADEЃНЁЯMNEЃЌ
ЁрЁїAEDЁзЁїMENЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрMNЃН![]() MEЃН
MEЃН![]() (Ѓm2ЃЋ
(Ѓm2ЃЋ![]() mЃЋ
mЃЋ![]() )ЃНЃ
)ЃНЃ![]() m2ЃЋ
m2ЃЋ![]() mЃЋ
mЃЋ![]() (Ѓ1ЁмmЁм
(Ѓ1ЁмmЁм![]() )ЃЌ
)ЃЌ
ЁрЕБ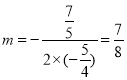 ЪБЃЌMNзюДѓЃЌЮЊ
ЪБЃЌMNзюДѓЃЌЮЊ![]() ЃЌ
ЃЌ
ДЫЪБMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ.
ЃЉ.
ЃЈ3ЃЉДцдкЃЌ
гЩЬтвзжЊЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ
Й§ЕуPзїPGЁЭyжсгкЕуGЃЌСЌНгOPЃЌ
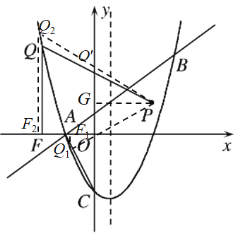
ШнвзЗЂЯжOGЃНOAЃН1ЃЌPGЃНOCЃН2ЃЌЁЯPGOЃНЁЯCOAЃН90ЁуЃЌ
ЁрЁїPGOЁеЁїCOAЃЌ
ЁрЁЯPOGЃНЁЯCAOЃЌ
бгГЄPOНЛХзЮяЯпгкЕуQ1ЃЌЙ§Q1зїQ1F1ЁЭxжсгкЕуF1ЃЌ
ДЫЪБЁЯF1Q1PЃНЁЯPOGЃНЁЯCAO.
взжЊжБЯпOPЕФНтЮіЪНЮЊ![]() ,
,
Сю![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Ёр![]() .
.
ЭЌРэЃЌдкyжсЩЯеввЛЕуOЁфЃЌЪЙOЁфGЃНOGЃН1ЃЌ
ШнвзжЄУїЁїPGOЁфЁеЁїCOAЃЌ
ЁрЁЯPOЁфGЃНЁЯCAOЃЌ
бгГЄPOЁфНЛХзЮяЯпгкЕуQ2ЃЌ
Й§ЕуQ2зїQ2F2ЁЭxжсгкЕуF2ЃЌ
ДЫЪБЃЌЁЯF2Q2PЃНЁЯPOЁфGЃНЁЯCAO.
взжЊжБЯпOЁфPЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Сю![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Ёр![]() .
.
ЁрЕуQЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ.
ЃЉ.