题目内容
【题目】(实验操作)如图①,在![]() 中,
中,![]() ,现将
,现将![]() 边沿
边沿![]() 的平分线
的平分线![]() 翻折,点
翻折,点![]() 落在
落在![]() 边的点
边的点![]() 处;再将线段
处;再将线段![]() 沿
沿![]() 翻折到线段
翻折到线段![]() ,连接
,连接![]() .
.
(探究发现)若点![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() 的大小是______,
的大小是______,![]() 的大小是________,此时三条线段
的大小是________,此时三条线段![]() ,
,![]() ,
,![]() 之间的数量关系是________.
之间的数量关系是________.
(应用拓展)如图②,将图①中满足(实验操作)与(探究发现)的![]() 的边
的边![]() 延长至
延长至![]() ,使得
,使得![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的度数.
的度数.


【答案】【探究发现】60°,100°,BC=BD+AD;【应用拓展】∠BCE=10°.
【解析】
探究发现:根据折叠性质可得∠ADB=∠BDA1,∠A1DC=∠CDA2,由B、D、A2在一条直线上可得∠CDA2=∠ADB,可得∠ADB=∠BDA1=∠A1DC=∠CDA2,根据平角定义可求出∠CDA2的度数即可得∠ADB的度数;根据外角性质及等腰三角形的性质即可求出∠BAC的度数;根据折叠性质可得AD=A1D=A2D,可得BD+AD=BA2,根据折叠性质可求出∠A2CB=∠BA2C,根据等腰三角形的性质即可得BC=BD+AD;应用拓展:以BC为边,在△ABC外作等边△BCD,连接AD,利用SSS可证明△ABD≌△ACD,可得∠ADB=∠ADC=![]() ∠BDC=30°,根据等腰三角形的性质可求出∠ABC=∠ACB=40°,可得∠ACD=∠BAC=100°,由AE=BC可得AE=CD,利用SAS可证明△AEC≌△CDA,可得∠AEC=∠ADC=30°,利用外角性质求出∠BCE的度数即可.
∠BDC=30°,根据等腰三角形的性质可求出∠ABC=∠ACB=40°,可得∠ACD=∠BAC=100°,由AE=BC可得AE=CD,利用SAS可证明△AEC≌△CDA,可得∠AEC=∠ADC=30°,利用外角性质求出∠BCE的度数即可.
探究发现:
∵![]() 边沿
边沿![]() 的平分线
的平分线![]() 翻折,点
翻折,点![]() 落在
落在![]() 边的点
边的点![]() 处,
处,
∴∠ADB=∠A1DB,
∵线段![]() 沿
沿![]() 翻折到线段
翻折到线段![]() ,
,
∴∠A1DC=∠A2DC,
∵B、D、A2三点共线,
∴∠ADB=∠A2DC,
∴∠A1DB=∠A1DC=∠A2DC,
∴∠A1DB=![]() ×180°=60°,
×180°=60°,
∴∠ADB=60°,
∵AB=AC,
∴∠ABC=![]() (180°-∠BAC),
(180°-∠BAC),
∵BD是∠ABC的角平分线,
∴∠ABD=![]() ∠ABC=
∠ABC=![]() (180°-∠BAC),
(180°-∠BAC),
∴∠BDC=∠ABD+∠BAC=![]() (180°-∠BAC)+∠BAC=120°,
(180°-∠BAC)+∠BAC=120°,
解得:∠BAC=100°,
根据折叠性质得:∠BA1D=∠BAC=100°,AD=A1D=A2D,∠BCA=∠ACA2=40°,
∴BD+AD=BD+A2D=BA2,∠A2=∠DA2C=180°-∠BA1D=80°,∠BCA2=2∠BCA=80°,
∴∠A2=∠BCA2,
∴BC=BA2,
∴BC=BD+AD.
故答案为:60°,100°,BC=BD+AD
应用拓展:
以BC为边,在△ABC外作等边△BCD,连接AD,
∴BC=BD=CD,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD,
∴∠ADB=∠ADC=![]() ∠BDC=30°,
∠BDC=30°,
∵∠ACB=∠ABC=40°,△BCD是等边三角形,
∴∠DCA=∠BAC=100°,
∵AE=BC,
∴AE=CD,
在△AEC和△CDA中,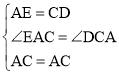 ,
,
∴△AEC≌△CDA,
∴∠AEC=∠ADC=30°,
∴∠BCE=∠ABC-∠AEC=40°-30°=10°.

 名校课堂系列答案
名校课堂系列答案







