题目内容
【题目】已知:四边形ABCD是一张矩形纸片,AB=3cm,BC=5cm

(1)在矩形ABCD的边AD上找一点E,使CE平分∠BED,请利用刻度尺或圆规作出点E,写出作法,并给出证明;
(2)把矩形纸片沿某直线剪一刀分成两部分后,再用这两部分拼成一个菱形,请画出剪拼的示意图,并求出菱形的较长对角线的长度.
【答案】(1)见解析;(2)见解析,![]()
【解析】
(1)如图1,利用“倒推法”,要作CE平分∠BED,就要∠BEC=∠DEC,而∠BCE=∠DEC,那么∠BCE=∠BEC,即BC=BE,只要作出BC=BE即可;
(2)如图2所示,沿BE裁剪,将△ABE平移至△DCF位置,由(1)知:四边形BCFE四边都相等,则四边形BCFE即为所求;在Rt△ABE中可求得AE的长,Rt△ABF中就可以求得AF的长,利用勾股定理可求得答案.
解:(1)如图1所示,点E即为所求;
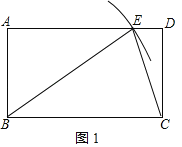
由作图知BC=BE,
∴∠BCE=∠BEC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCE=∠DEC,
∴∠BEC=∠DEC,
∴EC平分∠BED;
(2)如图2所示,沿BE裁剪,将△ABE平移至△DCF位置,则四边形BCFE即为所求,
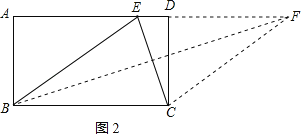
由(1)知:BC=BE=5,
∵AB=3,∠A=90°,
∴DF=AE=![]() =4,
=4,
则AF=AD+DF=5+4=9,
∴BF=![]() =3
=3![]() (cm).
(cm).

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目