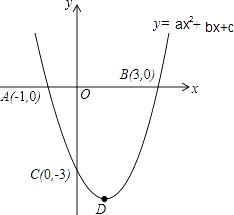��Ŀ����
����Ŀ�����ڡ�ABC�У�BC=a��AC=b��AB=c������C=90�㣬��ͼ1������a2+b2=c2������ABCΪ���������ʱ��С�����룺a2+b2��c2 �� �������£���ͼ2������A��AD��CB�ڵ�D����CD=x����Rt��ADC�У�AD2=b2��x2 �� ��Rt��ADB�У�AD2=c2����a��x��2
��a2+b2=c2+2ax
��a��0��x��0
��2ax��0
��a2+b2��c2
�൱��ABCΪ���������ʱ��a2+b2��c2
����С���IJ�������ȷ�ģ�
��1��������룬����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵ��
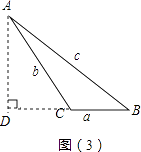
��2����ܰ��ʾ����ͼ3�У���BC���ϵĸߣ�
��3��֤�������Ľ����Ƿ���ȷ��
���𰸡�
��1��
�⣺����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵΪ��a2+b2��c2
��2��
�⣺��ͼ3������A��AD��BC�ڵ�D
��3��
�⣺֤������ͼ3����CD=x��
��Rt��ADC��AD2=b2��x2����Rt��ADB��AD2=c2����a+x��2
��a2+b2=c2��2ax
��a��0��x��0
��2ax��0
��a2+b2��c2
�൱��ABCΪ�۽�������ʱ��a2+b2��c2
����������1����������ɲ²⣺����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵΪ��a2+b2��c2����2������������������ߣ�����A��AD��BC�ڵ�D����3��Ȼ����CD=x���ֱ���Rt��ADC��Rt��ADB�У���ʾ��AD2 �� ����֤�ý��ۣ��������������ε��ۺ��⣮�����˹��ɶ����Լ������ε�������⣮ע�����������ǽ����Ĺؼ���
�����㾫����������Ĺؼ������������������߹�ϵ�����֪ʶ����������������֮�ʹ��ڵ����ߣ�����������֮��С�ڵ����ߣ������϶����������߶Σ�������������ε����ߣ�

 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�