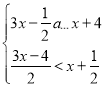��Ŀ����
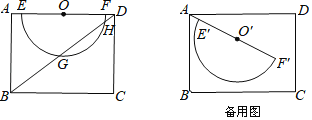
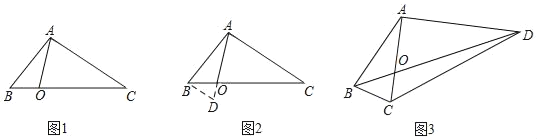
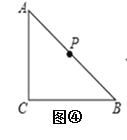
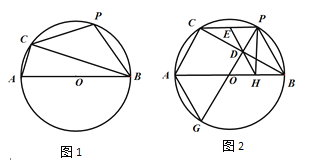
����Ŀ����ͼ1����б��ABΪֱ����Rt��ABC�����Բ��Բ��ΪO��PΪ��BC���е㣮
��1��ֻ��ֱ�ߺͱ���ͼ���ڻ�ACB��һ���Բ����һ��G������PG��BC�ڵ�D��ʹD��ΪBC�е㣮��˵��������ɣ�
��2���ڣ�1��С��ͼ�λ����ϣ���DG��ȡһ��K��ʹDK��DP������CK��BK���ж��ı���PBKC����״����֤����Ľ��ۣ�
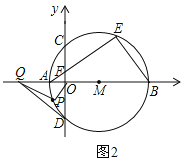
��3������ͼ2��ȡCP���е�E������ED���ӳ�ED��AB�ڵ�H������PH����֤������CAB��60��ʱ��HΪAB�ĵȷֵ㣮
���𰸡���1����ͼ�����������ɼ���������2���ı���PBKC�����Σ����ɼ���������3��������
��������
��1�����ݴ��������ɵã�����PO���ӳ���Բ�ڵ�G��Ϊ����
��2���ȸ��ݴ���������![]() ��
��![]() ���ٸ������ε��ж����ɵã�
���ٸ������ε��ж����ɵã�
��3���ȸ�����λ�߶����ó�![]() ���ٸ���Բ�ܽǶ�����ƽ���ߵ��ж��ó�
���ٸ���Բ�ܽǶ�����ƽ���ߵ��ж��ó�![]() ���Ӷ���
���Ӷ���![]() ��Ȼ�����ƽ���ߵ����ʡ����������ε����ʵó�
��Ȼ�����ƽ���ߵ����ʡ����������ε����ʵó�![]() ���Ӷ���
���Ӷ���![]() ����������λ�߶�����ֱ�������ε����ʵó�
����������λ�߶�����ֱ�������ε����ʵó�![]() ���ɴ˼��ɵ�֤��
���ɴ˼��ɵ�֤��
��1����ͼ������PO���ӳ���Բ�ڵ�G�����G��Ϊ�����������£�
��P�ǻ�BC���е�
��D��BC�е㣻����������)
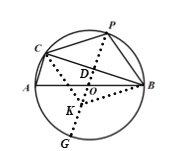
��2���ı���PBKC�����Σ�֤�����£�
�ɣ�1��֪��![]() ��
��![]() ������������
������������
��![]()
���ı���PBKC�����Σ��������Խ����ഹֱ�һ���ƽ�ֵ��ı��������Σ�
��3����![]()
��![]() ����
����![]()
��![]()
![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�ɣ�1��֪����DΪBC�е�
![]() Ϊ
Ϊ![]() ����λ��
�����
![]()
��![]() ��
�У�![]()
![]()
![]()
���HΪOB�е㣬��ΪAB�ĵȷֵ㣮

 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�