题目内容
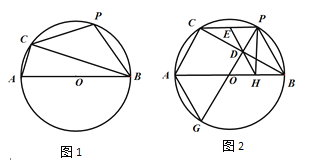
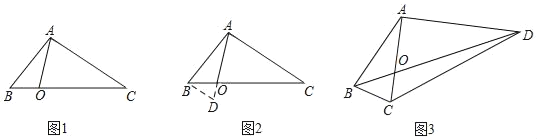
【题目】如图,(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=20°,∠OAC=80°,AO=![]() ,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
(2)请参考以上思路解决问题:如图3,在四边形ABCD中,对角线AC、BD相交于点O,AC⊥AD,AO=6![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
【答案】(1)80,8![]() ;(2)DC=8
;(2)DC=8![]()
【解析】
(1)根据平行线的性质可得∠ADB=∠OAC=80°,即可证明△BOD∽△COA,可得![]() ,求出AD的长度,再根据角的和差关系得∠ABD=180°﹣∠BAD﹣∠ADB=80°=∠ADB,即可得出AB=AD=8
,求出AD的长度,再根据角的和差关系得∠ABD=180°﹣∠BAD﹣∠ADB=80°=∠ADB,即可得出AB=AD=8![]() .
.
(2)过点B作BE∥AD交AC于点E,通过证明△AOD∽△EOB,可得![]() ,根据线段的比例关系,可得AB=2BE,根据勾股定理求出BE的长度,再根据勾股定理求出DC的长度即可.
,根据线段的比例关系,可得AB=2BE,根据勾股定理求出BE的长度,再根据勾股定理求出DC的长度即可.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=80°,
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]()
∵AO=6![]() ,
,
∴OD=![]() AO=2
AO=2![]() ,
,
∴AD=AO+OD=6![]() +2
+2![]() =8
=8![]() ,
,
∵∠BAD=20°,∠ADB=80°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=80°=∠ADB,
∴AB=AD=8![]() ,
,
故答案为:80,8![]() ;
;
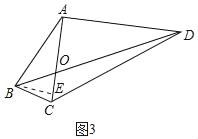
(2)过点B作BE∥AD交AC于点E,如图3所示:
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°,
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]()
∵BO:OD=1:3,
∴![]()
∵AO=6![]() ,
,
∴EO=![]() AO=2
AO=2![]() ,
,
∴AE=AO+EO=6![]() +2
+2![]() =8
=8![]() ,
,
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE,
在Rt△AEB中,BE2+AE2=AB2,即(8![]() )2+BE2=(2BE)2,
)2+BE2=(2BE)2,
解得:BE=8,
∴AB=AC=16,AD=3BE=24,
在Rt△CAD中,AC2+AD2=DC2,即162+242=DC2,
解得:DC=8![]() .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案