题目内容
【题目】(1)如图,已知△ABC中,AB=2,BC=4.画出△ABC的高AD和CE并求出![]() 的值.
的值.
(2)在平面直角坐标系中,O为坐标原点,点A的坐标为![]() ,点B坐标为
,点B坐标为![]() 满足
满足![]() .
.
①若![]() 没有平方根,判断点A在第几象限并说明理由;
没有平方根,判断点A在第几象限并说明理由;
②若点A到![]() 轴的距离是点B到
轴的距离是点B到![]() 轴距离的3倍,求点B的坐标.
轴距离的3倍,求点B的坐标.
【答案】(1)作图见详解,![]() ;(2)①点A在第二象限,②(3,1)或(6,﹣2).
;(2)①点A在第二象限,②(3,1)或(6,﹣2).
【解析】
(1)利用钝角三角形边上的高线作法,延长各边作出即可;利用三角形面积求法公式得出即可.
(2)①根据平方根的意义得到a<0,然后根据各象限点的坐标特征可判断点A在第二象限;②先利用方程组![]() ,用a表示b、c得b=a,c=4﹣a,则B点坐标为(a,4﹣a),再利用点A到x轴的距离是点B到x轴距离的3倍得到|﹣a|=3|4﹣a|,则a=3(4﹣a)或a=﹣3(4﹣a),分别解方程求出a的值,然后计算出c的值,于是可写出B点坐标.
,用a表示b、c得b=a,c=4﹣a,则B点坐标为(a,4﹣a),再利用点A到x轴的距离是点B到x轴距离的3倍得到|﹣a|=3|4﹣a|,则a=3(4﹣a)或a=﹣3(4﹣a),分别解方程求出a的值,然后计算出c的值,于是可写出B点坐标.
解:(1)如图所示,AD、CE即为所求:
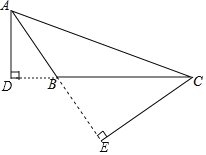
∵S△ABC=![]() ×AD×BC=
×AD×BC=![]() AB×CE,
AB×CE,
∴![]() .
.
(2)①点A在第二象限,
理由:∵a没有平方根
∴a<0、﹣a>0,
∴点A在第二象限;
②解方程组![]() .
.
用a表示b、c得:b=a,c=4﹣a,
∴B点坐标为(a,4﹣a),
∵点A到x轴的距离是点B到x轴距离的3倍,
∴|﹣a|=3|4﹣a|,
当a=3(4﹣a),解得a=3,则c=4﹣3=1,此时B点坐标为(3,1);
当a=﹣3(4﹣a),解得a=6,则c=4﹣6=﹣2,此时B点坐标为(6,﹣2);
综上所述,B点坐标为(3,1)或(6,﹣2).

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目