题目内容
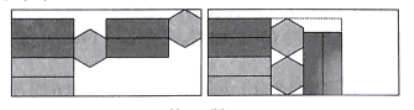
【题目】如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出![]() ,宽留出
,宽留出![]() 则该六棱柱的侧面积是( )
则该六棱柱的侧面积是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
设正六棱柱的底面边长为acm,高为hcm,分别表示出挪动前后所在矩形的长与宽,由题意列出方程求出a=2,h=9![]() ,再根据六棱柱的侧面积是6ah求解.
,再根据六棱柱的侧面积是6ah求解.
解:设正六棱柱的底面边长为acm,高为hcm,
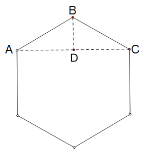
如图,正六边形边长AB=acm时,由正六边形的性质可知∠BAD=30°,
∴BD=![]() cm,AD=
cm,AD=![]() cm,
cm,
∴AC=2AD=![]() cm,
cm,
∴挪动前所在矩形的长为(2h+2![]() a)cm,宽为(4a+
a)cm,宽为(4a+![]() )cm,
)cm,
挪动后所在矩形的长为(h+2a+![]() )cm,宽为4acm,
)cm,宽为4acm,
由题意得:(2h+2![]() a)(h+2a+
a)(h+2a+![]() )=5,(4a+
)=5,(4a+![]() )4a=1,
)4a=1,
∴a=2,h=9![]() ,
,
∴该六棱柱的侧面积是6ah=6×2×(9![]() )=
)=![]() ;
;
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
甲 | 乙 | 丙 | |
数量(个) |
|
|
|
批发单价(元) |
|
|
|
|
![]() 当
当![]() 时,若这三种礼品共批发
时,若这三种礼品共批发![]() 个,甲礼品的总价不低于丙礼品的总价,求
个,甲礼品的总价不低于丙礼品的总价,求![]() 的最小值.
的最小值.
![]() 已知该店用
已知该店用![]() 元批发了这三种礼品,且
元批发了这三种礼品,且![]() .
.
![]() 当
当![]() 时,若批发这三种礼品的平均单价为
时,若批发这三种礼品的平均单价为![]() 元/个,求
元/个,求![]() 的值.
的值.
![]() 当
当![]() 时,若该店批发了
时,若该店批发了![]() 个丙礼品,且
个丙礼品,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.