题目内容
已知:如图,在梯形ABCD中,AB∥CD,AD=BC,AB=10,CD=18,∠ADC=60°,过BC上一点E作直线EH,交CD于点F,交AD的延长线于点H,且EF=FH.
(1)求梯形ABCD的面积;
(2)求证:AD=DH+BE.


(1)求梯形ABCD的面积;
(2)求证:AD=DH+BE.


(1)解:过点A作AG⊥CD于点G.
∵在梯形ABCD中,AD=BC,AB=10,CD=18,
∴DG=(18-10)÷2=4.
∵在Rt△ADG中,∠ADC=60°,
∴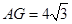 .
.
∴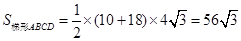
(2)证明:过点E作EM∥AD,交CD于点M,
∴ ∠H=∠FEM.
∵ EF=FH,∠DFH=∠EFM, ∴△DFH ≌△MFE.
∴ DH=EM.
∵ 四边形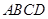 为等腰梯形, ∴ ∠C=∠ADC.
为等腰梯形, ∴ ∠C=∠ADC.
∵ EM∥AD, ∴∠ADC=∠EMC,∴ ∠C=∠EMC .
∴ EM=EC, ∴ DH=EC.
∵ BC=BE+EC, AD=BC, ∴ AD=BE+DH.
∵在梯形ABCD中,AD=BC,AB=10,CD=18,
∴DG=(18-10)÷2=4.
∵在Rt△ADG中,∠ADC=60°,
∴
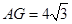 .
.∴
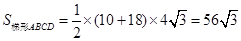
(2)证明:过点E作EM∥AD,交CD于点M,
∴ ∠H=∠FEM.
∵ EF=FH,∠DFH=∠EFM, ∴△DFH ≌△MFE.
∴ DH=EM.
∵ 四边形
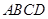 为等腰梯形, ∴ ∠C=∠ADC.
为等腰梯形, ∴ ∠C=∠ADC.∵ EM∥AD, ∴∠ADC=∠EMC,∴ ∠C=∠EMC .
∴ EM=EC, ∴ DH=EC.
∵ BC=BE+EC, AD=BC, ∴ AD=BE+DH.
(1)过点A作AG⊥CD于点G.利用勾股定理求出AG长,根据梯形的面积公式求解
(2)过点E作EM∥AD,交CD于点M,证得△DFH ≌△MFE.得出DH=EM.通过四边形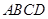 为等腰梯形,得出EM=EC,通过 AD=BC,得出结论
为等腰梯形,得出EM=EC,通过 AD=BC,得出结论
(2)过点E作EM∥AD,交CD于点M,证得△DFH ≌△MFE.得出DH=EM.通过四边形
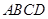 为等腰梯形,得出EM=EC,通过 AD=BC,得出结论
为等腰梯形,得出EM=EC,通过 AD=BC,得出结论
练习册系列答案
相关题目
 为何值时,四边形
为何值时,四边形 的面积是梯形
的面积是梯形 的面积的一半;
的面积的一半;
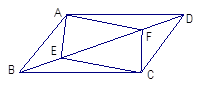

 ,AB=CD=AD=2,
,AB=CD=AD=2, ,则下底BC长是
,则下底BC长是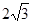

 于E,
于E, 于F,BD与AE、AF分别相交于G、H.
于F,BD与AE、AF分别相交于G、H. ,求证:四边形ABCD是菱形.
,求证:四边形ABCD是菱形.

 ABCD的一边BC延长至E,若∠A=110°,则∠1=________.
ABCD的一边BC延长至E,若∠A=110°,则∠1=________. [
[