题目内容
【题目】已知:直线y=![]() x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
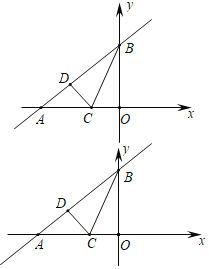
将△CBO沿BC折叠后,点O恰好落在AB边上点D处
(1)求直线BC的解析式;
(2)求点D的坐标;
(3)P为平面内一动点,且以A、B、C、P为顶点的四边形为平行四边形,直接写出点P坐标 .
【答案】(1)y=2x+3;(2)(﹣![]() ,
,![]() );(3)(﹣
);(3)(﹣![]() ,3)或(
,3)或(![]() ,3)或(﹣
,3)或(﹣![]() ,﹣3).
,﹣3).
【解析】
(1)先求出OA,OB,再利用勾股定理即可求出AB=5,由折叠的性质得出DC=OC,DB=OB=3,∠BDC=∠BOC=90°,设OC=DC=x,则AC=4-x,由勾股定理得出方程,求出OC的长,得出点C的坐标,由待定系数法即可得出答案;
(2)作DM⊥OA于M,则DM∥OB,得出△ADM∽△ABO,得![]() ,求出AM=
,求出AM=![]() ,DM=
,DM=![]() ,得出OM=OA-AM=4-
,得出OM=OA-AM=4-![]() =
=![]() ,即可得出答案;
,即可得出答案;
(3)分三种情况,利用平行四边形的性质,即可得出结论.
解:(1)∵直线![]() ,当x=0时,y=3;当y=0时,x=-4;
,当x=0时,y=3;当y=0时,x=-4;
∴A(-4,0),B(0,3),
∴OA=4,OB=3,
∴在Rt△AOB中,AB=![]() =5,
=5,
由折叠的性质得:DC=OC,DB=OB=3,∠BDC=∠BOC=90°,
∴AD=AB-DB=5-3=2,∠ADC=90°,
设OC=DC=x,则AC=4-x,
在Rt△ACD中,由勾股定理得:22+x2=(4-x)2,
解得:x=![]() ,
,
∴OC=![]() ,
,
∴C(![]() ,0),
,0),
设直线BC的解析式为y=kx+b,
把点B(0,3)、C(![]() ,0)代入得:
,0)代入得: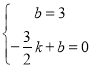 ,
,
解得:![]() ,
,
∴直线BC的解析式为y=2x+3;
(2)由(1)得:AD=2,作DM⊥OA于M,如图所示:
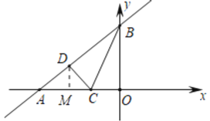
则DM∥OB,
∴△ADM∽△ABO,
∴![]() ,即
,即![]() ,
,
解得:AM=![]() ,DM=
,DM=![]() ,
,
∴OM=OA-AM=4-![]() =
=![]() ,
,
∴点D的坐标为![]() ;
;
(3)如图所示:
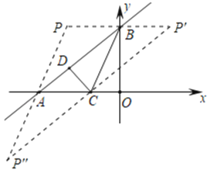
由(1)知,A(-4,0),B(0,3),C(![]() ,0),AC=4-
,0),AC=4-![]() =
=![]() ,
,
∵以A、B、C、P为顶点的四边形是平行四边形,
①当AC为边时,BP∥AC,BP=AC=![]() ,
,
∴P(![]() ,3)或(
,3)或(![]() ,3);
,3);
②当AC为对角线时,点B向下平移3个单位,再向左平移![]() 个单位得到C,
个单位得到C,
∴点A向下平移3个单位,再向左平移![]() 个单位得到点P的坐标(-4-
个单位得到点P的坐标(-4-![]() ,0-3),
,0-3),
∴P(-![]() ,-3),
,-3),
即:点P的坐标为(![]() ,3)或(
,3)或(![]() ,3)或(-
,3)或(-![]() ,-3);
,-3);
故答案为:(![]() ,3)或(
,3)或(![]() ,3)或(-
,3)或(-![]() ,-3).
,-3).

 启东小题作业本系列答案
启东小题作业本系列答案




