题目内容
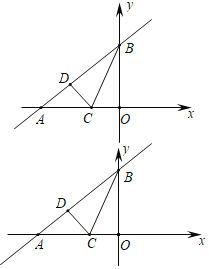
【题目】如图,⊙O 的内接四边形 ABCD 两组对边延长线分别交于点 E、F.
(1)若∠E=∠F,求证:∠ADC=∠ABC;
(2)若∠E=∠F=40°,求∠A 的度数;
(3)若∠E=30°,∠F=40°,求∠A 的度数.

【答案】(1)见解析;(2)50°;(3)55°.
【解析】
(1)根据外角的性质即可得到结论;
(2)根据圆内接四边形的性质和等量代换即可求得结果;
(3)连结EF,如图,根据圆内接四边形的性质得∠ECD=∠A,再根据三角形外角性质得∠ECD=∠1+∠2,则∠A=∠1+∠2,然后根据三角形内角和定理有∠A+∠1+∠2+∠E+∠F=180°,解方程即可.
(1)∠E=∠F,
∵∠DCE=∠BCF,
∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,
∴∠ADC=∠ABC;
(2)由(1)知∠ADC=∠ABC,
∵∠EDC=∠ABC,
∴∠EDC=∠ADC,
∴∠ADC=90°,
∴∠A=90°﹣40°=50°;
(3)连结 EF,如图,
∵四边形 ABCD 为圆的内接四边形,
∴∠ECD=∠A,
∵∠ECD=∠1+∠2,
∴∠A=∠1+∠2,
∵∠A+∠1+∠2+∠E+∠F=180°,
∴2∠A+30°+40°=180°,
∴∠A =55°.

 阅读快车系列答案
阅读快车系列答案【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择
单车”已成为很多市民出行的选择![]() 张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为
张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为![]() 单位:千米
单位:千米![]() ,乘坐地铁的时间为
,乘坐地铁的时间为![]() 单位分钟
单位分钟![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根据表中数据的规律,直接写出表格中a、b的值和
根据表中数据的规律,直接写出表格中a、b的值和![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 张老师骑单车的时间
张老师骑单车的时间![]() 单位:分钟
单位:分钟![]() 也受x的影响,其关系可以用
也受x的影响,其关系可以用![]() 米描述,
米描述,
![]() 若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
![]() 若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.