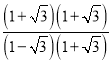题目内容
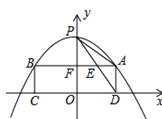
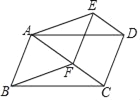
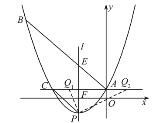
【题目】如图,已知抛物线![]() 经过
经过![]() 的三个顶点,其中点
的三个顶点,其中点![]() ,点
,点![]() ,
,![]() 轴,点
轴,点![]() 是直线
是直线![]() 下方抛物线上的动点.
下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点![]() 且与
且与![]() 轴平行的直线
轴平行的直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)当点![]() 为抛物线的顶点时,在直线
为抛物线的顶点时,在直线![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,若存在,求出点
相似,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
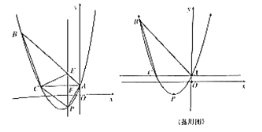
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)满足条件的点
;(3)满足条件的点![]() 有两个,坐标分别是
有两个,坐标分别是![]() 或
或![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据平行于x轴的直线上点的纵坐标相等,可得C点的纵坐标,根据自变量与函数值的对应关系,可得C点坐标,根据待定系数法,可得AB的解析式,根据直线上的点满足函数解析式,可得E点坐标,根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PE的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;
(3)根据等腰直角三角形的性质,可得∠PCF=∠EAF,根据相似三角形的判定,可得关于t的方程,根据解方程,可得答案.
解:(1)把点![]() ,
,![]() 的坐标代入
的坐标代入![]() ,
,
得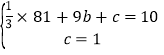 ,解得
,解得![]() .
.
∴抛物线的解析式是![]() .
.
(2)∵![]() 轴,
轴,![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() (舍),
(舍),
∴![]() .
.
设直线![]() 的解析式是
的解析式是![]() ,
,
由![]() ,解得
,解得![]() .
.
则直线![]() 的解析式是
的解析式是![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]() .
.
又∵![]() ,
,
则当![]() 时,四边形
时,四边形![]() 的面积的最大值是
的面积的最大值是![]() ,
,
此时点![]() 的坐标是
的坐标是![]() .
.
(3)由![]() ,得顶点
,得顶点![]() 的坐标是
的坐标是![]() ,此时
,此时![]() ,
,![]() ,
,
则在![]() 中,
中,![]() ,∴
,∴![]() .
.
同理可求![]() ,∴
,∴![]() ,
,
∴在直线![]() 上存在满足条件的
上存在满足条件的![]() ,如图
,如图![]() 或
或![]() .
.
可求![]() ,
,![]() ,
,![]() ,
,
①当![]() 时,设
时,设![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() .
.
②当![]() ,设
,设![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() .
.
综上,满足条件的点![]() 有两个,坐标分别是
有两个,坐标分别是![]() 或
或![]() .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
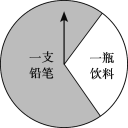
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.