Question

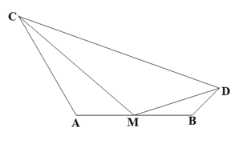
【题目】如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，

（1）问直线EF与AB有怎样的位置关系？加以证明；

（2）若∠CEF=70°，求∠ACB的度数．

Answer 1

【答案】（1）EF和AB的关系为平行关系；（2）∠ACB=40°．

【解析】

（1）由平行线的性质推出∠DCB=∠ABC=70°，结合∠CBF=20°，推出∠ABF=50°，即可得出∠EFB+∠ABF=180°，根据平行线的判定即可推出EF∥AB；

（2）根据（1）推出的结论，推出EF∥CD，根据平行线的性质推出∠ECD=110°，根据∠DCB=70°，即可求出∠ACB的度数．

解：（1）EF和AB的关系为平行关系．理由如下：

∵CD∥AB，∠DCB=70°，

∴∠DCB=∠ABC=70°，

∵∠CBF=20°，

∴∠ABF=∠ABC﹣∠CBF=50°，

∵∠EFB=130°，

∴∠ABF+∠EFB=50°+130°=180°，

∴EF∥AB；

（2）∵EF∥AB，CD∥AB，

∴EF∥CD，

∵∠CEF=70°，

∴∠ECD=110°，

∵∠DCB=70°，

∴∠ACB=∠ECD﹣∠DCB，

∴∠ACB=40°．