题目内容
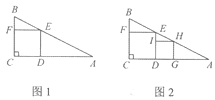
【题目】正方形![]() 中,
中,![]() 为过顶点A的任意一条射线,过C作
为过顶点A的任意一条射线,过C作![]() 于E.
于E.

(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)过D作![]() 于F,过C作
于F,过C作![]() 于H,求证:
于H,求证:![]() .
.
【答案】(1)2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据正方形及勾股定理先求出AC的长度,再利用勾股定理,可求CE的长;
(2)证明△ADF≌△DCH,得到DF=CH,接着证明四边形CEFH为矩形,从而有CH=EF,最后得到DF=EF.
(1)解:正方形ABCD中,AB=6,
∴BC=6,∠ABC=90°,∴AC=6![]() .
.
∵CE⊥AE,
∴CE=![]() ,
,
即CE=2![]() ;
;
(2)证明:∵CE⊥AE,DF⊥AE,CH⊥DF,
∴∠HFE=∠CHF=∠CEF=90°,
∴四边形CEFH为矩形,
∴CH=EF,
∵∠ADH+∠HDC=∠HDC+∠DCH=90°,
∴∠ADH=∠DCH,
在△ADF和△DCH中,
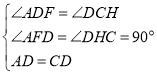 ,
,
∴△ADF≌△DCH(AAS),
∴DF=CH,
∴DF=EF.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】甲、乙两个商场在同一周内经营同一种商品,每天的获利情况如下表:
日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 |
甲商场获利/万元 | 2.5 | 2.4 | 2.8 | 3 | 3.2 | 3.5 | 3.6 |
乙商场获利/万元 | 1.9 | 2.3 | 2.7 | 2.6 | 3 | 4 | 4.5 |
(1)请你计算出这两个商场在这周内每天获利的平均数,并说明这两个商场本周内总的获利情况;
(2)在图所示的网格图内画出两个商场每天获利的折线图;(甲商场用虚线,乙商场用实线)
(3)根据折线图,请你预测下周一哪个商场的获利会多一些并简单说出你的理由.