题目内容
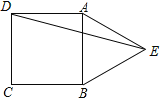
【题目】如图1是“东方之星”救援打捞现场图,小红据此构造出一个如图2所示的数学模型,已知:A、B、D三点在同一水平线上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.
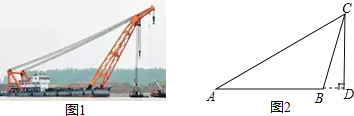
(1)求点B到AC的距离;
(2)求线段CD的长度.
【答案】(1)30m,(2)(15+15![]() )m.
)m.
【解析】
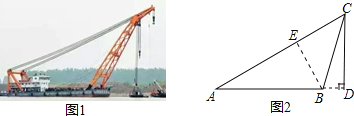
试题分析:过点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长,由AE+CE求出AC的长,即可求出CD的长.
解:过点B作BE⊥AC于点E,
在Rt△AEB中,AB=60m,sinA=![]() ,BE=ABsinA=60×
,BE=ABsinA=60×![]() =30,cosA=
=30,cosA=![]() ,
,
∴AE=60×![]() =30
=30![]() m,
m,
在Rt△CEB中,∠ACB=∠CBD﹣∠A=75°﹣30°=45°,
∴BE=CE=30m,
∴AC=AE+CE=(30+30![]() )m,
)m,
在Rt△ADC中,sinA=![]() ,
,
则CD=(30+30![]() )×
)×![]() =(15+15
=(15+15![]() )m.
)m.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?