Question

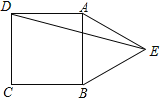
【题目】如图，等边△ABE与正方形ABCD有一条共公边，点E在正方形外，连结DE，则∠BED= °．

Answer 1

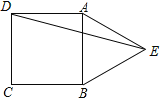
【答案】45°

【解析】

试题分析：根据正方形的性质，可得AB与AD的关系，∠BAD的度数，根据等边三角形的性质，可得AE与AB的关系，∠AEB的度数，根据等腰三角形的性质，可得∠AED与∠ADE的关系，根据三角形的内角和，可得∠AED的度数，根据角的和差，可得答案．

解：∵四边形ABCD是正方形，

∴AB=AD，∠BAD=90°，

∵等边三角形ABE，

∴AB=AE，∠BAE=∠AEB=60°，

∠DAE=∠BAD+∠BAE=90°+60°=150°，

AD=AE，

∴∠AEB=∠ABE=（180°﹣∠DAB）÷2=15°，

∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°，

故答案为：45°