题目内容
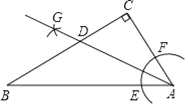
【题目】如图，在△ABC中，∠C=90°，AB=8，AC=4，以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F，再分别以点E、F为圆心，大于EF长为半径画弧，两弧交于点G，作射线AG，交BC于点D，则D到AB的距离为（ ）
A. 2 B. 4 C. 
D. 
【答案】C
【解析】如图，作DH⊥AB于H，设DM=DC=x，由S△ABC=S△ADC+S△ADB，可得
ACBC=ABDM+CDAC，列出方程即可解决问题．
解：如图，作DH⊥AB于H，
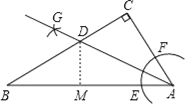
由题意∠DAC=∠DAB，∵DC⊥AC．DM⊥AB，
∴DC=DM，设DM=DC=x，
在Rt△ABC中，BC=
=4
，
∵S△ABC=S△ADC+S△ADB，
∴
ACBC=ABDM+CDAC，
∴44
=8x+4x，
∴x=
，
∴DM=，
故选C．
练习册系列答案
相关题目
【题目】据报道，某公司的33名职工的月工资如下（单位：元）：
职务 | 董事长 | 副董事长 | 总经理 | 董事 | 经理 | 管理员 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5500 | 5000 | 3500 | 3230 | 2730 | 2200 | 1500 |
（1）该公司职工的月工资的平均数=元、中位数=元、众数=元．
（2）假设副董事长的工资从5 000元涨到15 000元，董事长的工资从5 500元涨到28 500元，那么新的平均工资=元、中位数=元、众数=元．（精确到1元）
（3）你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平？
