Question

【题目】如图,在直角 ABC中， ACB=90 ， =60 ，AD，CE分别是 BAC和 BCA的平分线，AD，CE相交于点F．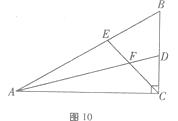

（1）求 EFD的度数；
（2）判FE与FD之间的数量关系，并证明你的结论．

Answer 1

【答案】
（1）解：如图所示，
∵在△ABC中，∠ACB=90°，∠B=60°，
∴∠BAC=30°
∵AD ， CE分别是∠BAC和∠BCA的平分线，
∴∠FAC= ∠BAC=15°，∠FCA= ∠ACB=45°.
∴∠AFC=180°∠FAC∠FCA=120°，
∴∠EFD=∠AFC=120° 。
（2）解：结论：FE=FD.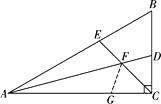

理由是：如图，在AC上截取AG＝AE ， 连接FG ，
∵AD是∠BAC的平分线，
∴∠EAF=∠GAF.
在△AEF和△AGF中，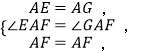

∴△AEF≌△AGF(SAS)，
∴FE=FG ， ∠AFE=∠AFG ，
∵∠EFD=120°，
∴∠DFC=60°，∠AFG=∠AFE=60°，
∴∠CFG=60°=∠DFC.
∵EC平分∠BCA ，
∴∠DCF=∠FCG=45°.
在△FGC和△FDC中，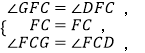

∴△FGC≌△FDC(ASA)，
∴FG=FD ，
∴FE=FD.
【解析】（1）根据三角形的内角和得出∠BAC=30°，根据角平分线的定义得出∠FAC= ∠BAC=15°，∠FCA= ∠ACB=45°.根据三角形的内角和得出∠AFC=180°∠FAC∠FCA=120°，根据对顶角相等得出∠EFD=∠AFC=120°；
（2）结论：FE=FD.理由是：如图，在AC上截取AG＝AE ， 连接FG ， 根据角平分线定义得出∠EAF=∠GAF.然后利用SAS判断出△AEF≌△AGF，然后根据全等三角形对应角相等，对应边相等得出FE=FG ， ∠AFE=∠AFG ， 根据邻补角的定义得出∠DFC=60°，∠AFG=∠AFE=60°，进而得出∠CFG=60°=∠DFC.根据角的角平分线的定义得出∠DCF=∠FCG=45°.然后利用ASA判断出△FGC≌△FDC，根据全等三角形对应边相等得出FG=FD ， 根据等量代换得出答案。