题目内容
【题目】同学们知道：“在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°．”
（1）请写出它的逆命题 ；该逆命题是一个 命题（填“真”或“假”）
（2）若你的判断是真命题请写出证明过程（要求画图，并写出已知，求证）．若是假命题，请说明理由．
【答案】（1）在直角三角形中，如果一个锐角等于30度，那么它所对的直角边等于斜边的一半，真；（2）已知，在Rt△ABC中，∠A＝30°，∠ACB＝90°．求证：BC＝
AB．
【解析】
（1）写出逆命题，并判断是真命题；
（2）首先写出已知、求证，画出图形，借助等边三角形的判定和性质证明或借助三角形的外接圆证明．
解：（1）原命题的逆命题为：在直角三角形中，如果一个锐角等于30度，那么它所对的直角边等于斜边的一半，该逆命题是一个真命题；
（2）已知，在Rt△ABC中，∠A＝30°，∠ACB＝90°．
求证：BC＝AB．
证明：
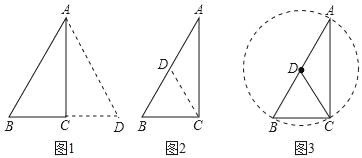
证法一：如图1所示，延长BC到D，使CD＝BC，连接AD，易证AD＝AB，∠BAD＝60°．
∴△ABD为等边三角形，
∴AB＝BD，
∴BC＝CD＝AB，即BC＝AB．
证法二：如图2所示，取AB的中点D，
连接DC，有CD＝AB＝AD＝DB，
∴∠DCA＝∠A＝30°，∠BDC＝∠DCA+∠A＝60°．
∴△DBC为等边三角形，
∴BC＝DB＝AB，即BC＝AB．
证法三：如图3所示，在AB上取一点D，使BD＝BC，
∵∠B＝60°，
∴△BDC为等边三角形，
∴∠DCB＝60°，∠ACD＝90°﹣∠DCB＝90°﹣60°＝30°＝∠A．
∴DC＝DA，即有BC＝BD＝DA＝AB，
∴BC＝AB．
证法四：如图3所示，作△ABC的外接圆⊙D，∠C＝90°，AB为⊙O的直径，
连DC，有DB＝DC，∠BDC＝2∠A＝2×30°＝60°，
∴△DBC为等边三角形，
∴BC＝DB＝DA＝AB，即BC＝AB．
