题目内容
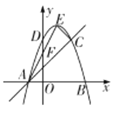
【题目】如图,点P为抛物线L:y=a(x﹣2)(x﹣4)(其中a为常数,且a<0)的顶点,L与y轴交于点C,过点C作x轴的平行线,与L交于点A,过点A作x轴的垂线,与射线OP交于点B,连接OA
(1)a=﹣2时,点P的坐标是 ,点B的坐标是 ;
(2)是否存在a的值,使OA=OB?若存在,求出a的值;若不存在,请说明理由
(3)若△OAB的外心N的坐标为(p,q),则
①当点N在△OAB内部时,求a的取值范围;
②用a表示外心N的横坐标p和纵坐标q,并求p与q的关系式(不写q的取值范围).
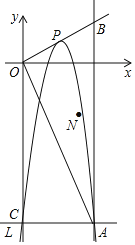
【答案】(1)(3,2),(6,4);(2)不存在,见解析;(3)①﹣![]() <a<0;②N横坐标p=
<a<0;②N横坐标p=![]() a2+3,N纵坐标q=3a ;p=
a2+3,N纵坐标q=3a ;p=![]() q2+3
q2+3
【解析】
(1)按照题意逐步计算:先把a=﹣2代入抛物线求出顶点P及与y轴交点C的坐标,得到直线OP解析式.由AC∥x轴可知A、C关于抛物线对称轴对称,进而求出点A.由AB⊥x轴可得B的横坐标与A相同,再代回直线OP即求得B的纵坐标.
(2)按照(1)的解题思路,先用a表示点P、C,然后得到点A坐标,即得到点B横坐标,再代回直线OP求得点B坐标.由于点A、B到x轴距离不相等,x轴不能垂直平分AB,故不存在a使OA=OB.
(3)①锐角三角形的外心会落在三角形内部,而∠OAB与∠OBA一定小于90°,则∠AOB<90°,可得OA2+OB2>AB2,把含a的式子代入即得到关于a的不等式,结合a<0得到a的取值范围;
②外心N为△OAB三边垂直平分线交点,由AB⊥x轴即可得点N纵坐标q=3a,由ON=AN列得关于a、p的等式,整理即得到用a表示p.再把a=![]() q代入即得到p关于q的关系式.
q代入即得到p关于q的关系式.
解:(1)∵a=﹣2
∴抛物线L:y=﹣2(x﹣2)(x﹣4)=﹣2x2+12x﹣16=﹣2(x﹣3)2+2
∴顶点P(3,2),C(0,﹣16)
∴直线OP解析式为:y=![]() x
x
∵AC∥x轴
∴yA=yC=﹣16,A、C关于直线x=3对称
∴A(6,﹣16)
∵AB⊥x轴
∴xB=xA=6
∴yB=![]() ×6=4,即B(6,4)
×6=4,即B(6,4)
故答案为:(3,2);(6,4).
(2)不存在a的值使OA=OB,理由如下:
∵抛物线L:y=a(x﹣2)(x﹣4)=ax2﹣6ax+8a=a(x﹣3)2﹣a
∴顶点P(3,﹣a),C(0,8a)
∴直线OP解析式为:y=﹣![]() x
x
∴A(6,8a)
∴yB=﹣![]() ×6=﹣2a
×6=﹣2a
∵a≠0
∴|yA|≠yB,即x轴不平分AB
∴OA≠OB
(3)①∵△OAB的外心N在其内部
∴△OAB是锐角三角形
∴∠AOB<90°
∴OA2+OB2>AB2
∵A(6,8a),B(6,﹣2a)
∴62+(8a)2+62+(﹣2a)2>(8a+2a)2
解得:﹣![]() <a<0
<a<0
②∵外心N在AB的垂直平分线上,AB⊥x轴
∴q=![]() =3a
=3a
∴N(p,3a),a=![]()
∵ON=AN,即ON2=AN2
∴p2+(3a)2=(6﹣p)2+(8a﹣3a)2
整理得:p=![]() a2+3
a2+3
把a=![]() 代入得:p=
代入得:p=![]() q2+3.
q2+3.

【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?