题目内容
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.

【答案】2![]() .
.
【解析】
过点G作GH⊥AD于H,根据翻折变换的性质可得GF⊥AE,然后求出∠GFH=∠D,再利用“角角边”证明△ADE和△GHF全等,根据全等三角形对应边相等可得GF=AE,再利用勾股定理列式求出AE,从而得解.
如图,过点G作GH⊥AD于H,
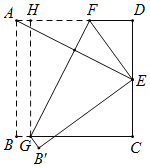
则四边形ABGH中,HG=AB,
由翻折变换的性质得GF⊥AE,
∵∠AFG+∠DAE=90°,∠AED+∠DAE=90°,
∴∠AFG=∠AED,
∵四边形ABCD是正方形,
∴AD=AB,
∴HG=AD,
在△ADE和△GHF中,
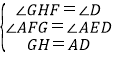 ,
,
∴△ADE≌△GHF(AAS),
∴GF=AE,
∵点E是CD的中点,
∴DE=![]() CD=2,
CD=2,
在Rt△ADE中,由勾股定理得,AE=![]() ,
,
∴GF的长为2![]() .
.
故答案为:2![]() .
.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目