题目内容
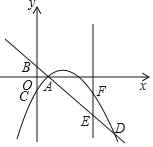
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,且
,且![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④关于
;④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() ,其中正确的结论个数有( )
,其中正确的结论个数有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】C
【解析】
由二次图像开口方向、对称轴与y轴的交点可判断出a、b、c的符号,从而可判断①;由图像可知当x=3时,y<0,可判断②;由OA=OC,且OA<1,可判断③;把﹣![]() 代入方程整理得ac2-bc+c=0,结合③可判断④;从而得出答案.
代入方程整理得ac2-bc+c=0,结合③可判断④;从而得出答案.
由图像开口向下,可知a<0,与y轴的交点在x轴的下方,可知c<0,又对称轴方程为x=2,∴﹣![]() >0,∴b>0,∴abc>0,故①正确;由图像可知当x=3时,y>0,∴9a+3b+c>0,故②错误;由图像可知OA<1,∵OA=OC,∴OC<1,即﹣c<1,故③正确;假设方程的一个根为x=﹣
>0,∴b>0,∴abc>0,故①正确;由图像可知当x=3时,y>0,∴9a+3b+c>0,故②错误;由图像可知OA<1,∵OA=OC,∴OC<1,即﹣c<1,故③正确;假设方程的一个根为x=﹣![]() ,把﹣
,把﹣![]() 代入方程,整理得ac2-bc+c=0, 即方程有一个根为x=﹣c,由②知﹣c=OA,而当x=OA是方程的根,∴x=﹣c是方程的根,即假设成立,故④正确.故选C.
代入方程,整理得ac2-bc+c=0, 即方程有一个根为x=﹣c,由②知﹣c=OA,而当x=OA是方程的根,∴x=﹣c是方程的根,即假设成立,故④正确.故选C.

【题目】为传承经典,某市开展“中华古诗词”朗读大赛,某中学甲、乙两名选手经过八轮预赛后脱颖而出,甲、乙两名学生的成绩如图所示,甲、乙两名学生成绩的相关统计数据如表所示,请结合图表回答下列问题:

平均数 | 方差 | |
甲 |
| 118.25 |
乙 | 80 |
|
(1)甲、乙两名同学预赛成绩的中位数分别是:甲__________分,乙___________分;
(2)王老师说,两个人的平均水平相当,不知道选谁参加决赛,但李老师说,乙同学的成绩稳定,请你先计算出![]() 的值并选择所学过的平均数、方差等统计知识,对两位老师的观点进行解释;
的值并选择所学过的平均数、方差等统计知识,对两位老师的观点进行解释;
(3)若学校想从两名选手中选择一名冲击决赛金牌,会选择谁参加?请说明理由.
【题目】某学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制作了不完整的统计图表.
学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 6 | 15 | a | 12 | 9 |
学生借阅图书的次数扇形统计图

请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该样本数据的中位数是 次,众数是 次;
(3)请计算扇形统计图中“3次”所对应的扇形圆心角的度数;
(4)若该校共有2400名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.