��Ŀ����
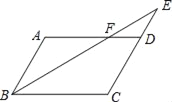
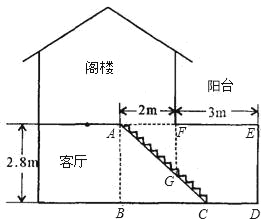
����Ŀ������ʦҪװ���Լ�����¥���¾ӣ���ͼΪ�¾�����ͼ�����ڽ����������¥��¥��ACʱ��Ϊ������¥ʱǽ��F��ͷ�����ǽ��F��¥�ݵ���ֱ����FGΪ1.75m�������ÿ�����AB=2.8m��¥�ݶ��ڿ�AF=2m����¥��̨��EF=3m�������������ʦ����������⣺
��1��Ҫʹǽ��F��¥�ݵ���ֱ����FGΪ1.75m��¥�ݵ�C��ǽ��D�ľ���CD�Ƕ����ף�
��2���ڣ�1���������£�Ϊ��֤��¥ʱ�����ʸУ�¥�ݵ�ÿ��̨��С��20cm��ÿ��̨��Ҫ����20cm��������ʦӦ�ý�¥�ݽ�����̨�ף�Ϊʲô��
���𰸡���1��CD=1.8m����2��¥��Ӧ��15��̨�ף������������.
��������
��1������Ϊ�ۺ���ʵ��Ӧ���⣬������ĿҪ��������������������֡�ABC�ס�GFA���Ӷ������CD��ֵ;��2�����������в���ʽ������⣮�п��й���ʵ�ʾ��������Ӧ����Ϊһ���ȵ㣬��Ŀ���ֶ࣬���ݶࡢ������ϵ�࣬����������⣬�г�����ʽ�������ǹؼ���������Ҫ�ڸ�������������Ʋ�ͬ�ķ����������Ƚ����ţ�Ѱ����ѷ�����
��1������������AF��BC
���ACB=��GAF��
����ABC=��AFG=90��
���ABC�ס�GFA��
��![]() ,
,
��![]() ��
��
��BC=3.2��m��
CD=��2+3����3.2=1.8��m����
��2����¥��Ӧ��n��̨�ף���![]() ,
,
���14��n��16��
��n��������
��¥��Ӧ��15��̨�ף�

����Ŀ��С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С�۵�̽�����̣��벹����ɣ�
��1������![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ��______________��
��ȡֵ��Χ��______________��
��2���б����ҳ�![]() ��
��![]() �ļ����Ӧֵ��
�ļ����Ӧֵ��
x | �� | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | b | 1 | 0 | 1 | 2 | �� |
����![]() ______________��
______________��
��3����ƽ��ֱ������ϵ![]() �У�������ϱ��и��Զ�ӦֵΪ����ĵ㣬�������ú�����ͼ��
�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣬�������ú�����ͼ��
��4������y=|x��1|����СֵΪ____________��