题目内容
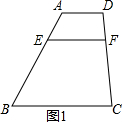 如图1,梯形ABCD中,AD∥BC,BC=a,AD=b,点E、F分别是两腰AB、CD上的点,且EF∥AD,设AE=d1、BE=d2,
如图1,梯形ABCD中,AD∥BC,BC=a,AD=b,点E、F分别是两腰AB、CD上的点,且EF∥AD,设AE=d1、BE=d2,
研究、发现:
(1)当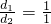 时,有EF=
时,有EF=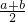 ;
;
当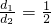 时,有EF=
时,有EF=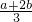 ;
;
当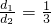 时,有EF=
时,有EF=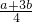 ;
;
(2)当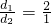 时,有EF=
时,有EF=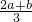 ;当
;当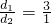 时,有EF=
时,有EF=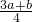 ;
;
当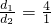 时,有
时,有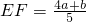 .
.
填空:①当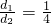 时,有EF=______;当
时,有EF=______;当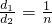 时,EF=______.
时,EF=______.
猜想、证明
②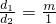 时,分别能得到什么结论(其中m、n均为正整数)并证明你的结论;
时,分别能得到什么结论(其中m、n均为正整数)并证明你的结论;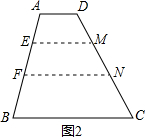
③进一步猜想当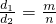 时,有何结论(其中m、n均为正整数)写出你的结论.
时,有何结论(其中m、n均为正整数)写出你的结论.
解决问题
(3)如图2,有一块梯形木框ABCD,AD∥BC,AD=1米,BC=3米,AB=5米,要在中间加两个横档.操作如下:在AD上取两点E、F,使AE=2米,EF=1.5米,分别从E、F两处做与两底平行的横档EM、FN,求需要木条的总长.
解:(1)当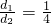 时,EF=
时,EF=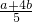 ;
;
当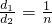 时,EF=
时,EF=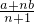 ;
;
当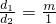 时,EF=
时,EF= .
.
当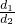 =
=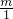 时,EF=
时,EF= .
.
证明:作AG∥CD交BC于点G,交EF于点H,
∵EF∥BC,
∴△AEH∽△ABG.
因为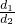 =
=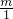 ,
,
所以, ,∴
,∴ ,
,
∴ .
.
(2)当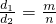 时,EF=
时,EF=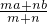 .
.
(3)因为AE:BE=2:3,由(2)中的结论可得:
EM= (米)
(米)
由于AF:BF=3.5:1.5=7:3,
由(2)中的结论可得:
FN= (米)
(米)
故两木条的总长度是1.8+2.4=4.2(米).
分析:①根据上述具体式子,即可发现规律,写出结论;
②首先根据具体式子,发现规律,写出结论;作平行线,构造一个平行四边形和三角形,根据平行四边形的性质和相似三角形的性质进行求解;
③综合上述结论,即可猜想到EF的结果;
④利用上述结论,求得EM和FN的长.
点评:此题综合运用了平行四边形的性质和相似三角形的性质,进行探索结论.能够根据探索的结论进行有关的计算.
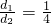 时,EF=
时,EF=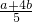 ;
;当
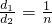 时,EF=
时,EF=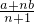 ;
;当
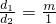 时,EF=
时,EF= .
.当
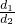 =
=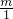 时,EF=
时,EF= .
.证明:作AG∥CD交BC于点G,交EF于点H,
∵EF∥BC,
∴△AEH∽△ABG.
因为
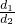 =
=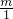 ,
,所以,
 ,∴
,∴ ,
,∴
 .
.(2)当
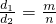 时,EF=
时,EF=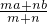 .
.(3)因为AE:BE=2:3,由(2)中的结论可得:
EM=
 (米)
(米)由于AF:BF=3.5:1.5=7:3,
由(2)中的结论可得:
FN=
 (米)
(米)故两木条的总长度是1.8+2.4=4.2(米).
分析:①根据上述具体式子,即可发现规律,写出结论;
②首先根据具体式子,发现规律,写出结论;作平行线,构造一个平行四边形和三角形,根据平行四边形的性质和相似三角形的性质进行求解;
③综合上述结论,即可猜想到EF的结果;
④利用上述结论,求得EM和FN的长.
点评:此题综合运用了平行四边形的性质和相似三角形的性质,进行探索结论.能够根据探索的结论进行有关的计算.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.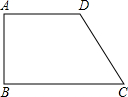 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形? 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=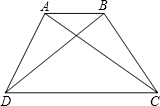 如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积.
如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积. 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=