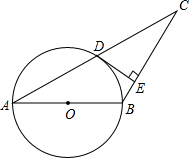
题目内容
如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.
求证:∠ACB=
∠OAC.

求证:∠ACB=
| 1 |
| 3 |

证明:连接OE、AE,并过点A作AF⊥DE于点F,(3分)
∵DE是圆的一条切线,E是切点,
∴OE⊥DC,(1分)
又∵BC⊥DE,
∴OE∥AF∥BC.(1分)
∴∠1=∠ACB,∠2=∠3.(1分)
∵OA=OE,
∴∠4=∠3.(1分)
∴∠4=∠2.(1分)
又∵点A是OB的中点,
∴点F是EC的中点.(1分)
∴AE=AC.(1分)
∴∠1=∠2.(1分)
∴∠4=∠2=∠1.(1分)
即∠ACB=
∠OAC.
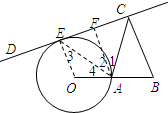
∵DE是圆的一条切线,E是切点,
∴OE⊥DC,(1分)
又∵BC⊥DE,
∴OE∥AF∥BC.(1分)
∴∠1=∠ACB,∠2=∠3.(1分)
∵OA=OE,
∴∠4=∠3.(1分)
∴∠4=∠2.(1分)
又∵点A是OB的中点,
∴点F是EC的中点.(1分)
∴AE=AC.(1分)
∴∠1=∠2.(1分)
∴∠4=∠2=∠1.(1分)
即∠ACB=
| 1 |
| 3 |


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目


 于点E.
于点E. AB=m.试求:
AB=m.试求: