题目内容
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
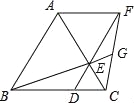
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.

练习册系列答案
相关题目