题目内容
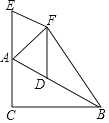
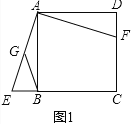
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
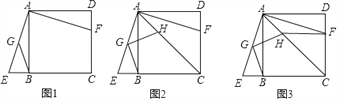
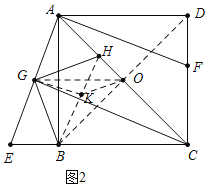
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)5.
【解析】试题分析:(1)如图1中,由△ABE≌△ADF,推出∠AFD=∠E,由AG=GE,推出GB=GE=GA,推出∠E=∠GBE=∠AFD,由∠GBE+∠GBC=180°,推出∠AFD+∠GBC=180°即可;
(2)如图2中,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK.只要证明O、H、G、B四点共圆,由AG=GE,AO=OC.推出OG∥CE,推出∠GOB=∠OBC=45°,即可解决问题;
(3)如图3中,如图3中,设OG交AB于T,GH交AB于P.,作HM⊥DF于M.只要证明∠EAB=∠GBP=∠PGT=∠HBO,推出tan∠EAB=tan∠HBO=![]() ,由CH=3AH,OA=OC=OB,推出tan∠EAB=tan∠HBO=
,由CH=3AH,OA=OC=OB,推出tan∠EAB=tan∠HBO=![]() =
=![]() ,BE=DF=
,BE=DF=![]() ,在RtHMF中,利用勾股定理即可解决问题.
,在RtHMF中,利用勾股定理即可解决问题.
试题解析:(1)如图1,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠AEF=90°,
∴∠EAB=∠DAF,∵∠ABE=∠ADF=90°,∴△ABE≌△ADF,∴∠AFD=∠E,
∵AG=GE,∴GB=GE=GA,∴∠E=∠GBE=∠AFD,∵∠GBE+∠GBC=180°,∴∠AFD+∠GBC=180°;
(2)如图2,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK,
∵∠BGH=∠BOH=90°,BK=KH,∴GK=KH=OK=KB,∴O、H、G、B四点共圆,
∵AG=GE,AO=OC,∴OG∥CE,
∴∠GOB=∠OBC=45°,∴∠GOH=∠GBH=45°,∵∠BGH=90°,
∴∠GBH=∠GHB=45°, ∴GH=GB;
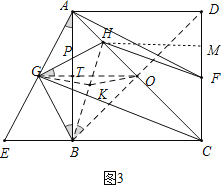
(3)如图3,设OG交AB于T,GH交AB于P,作HM⊥DF于M,
∵OG∥EC,AB⊥CE,∴OG⊥AB,易证∠EAB=∠GBP=∠PGT=∠HBO,
∴tan∠EAB=tan∠HBO=![]() ,∵CH=3AH,OA=OC=OB,∴tan∠EAB=tan∠HBO=
,∵CH=3AH,OA=OC=OB,∴tan∠EAB=tan∠HBO=![]() =
=![]() ,
,
∵AB=AD=2![]() ,∴BE=DF=
,∴BE=DF=![]() ,在Rt△HMF中,易证FM=
,在Rt△HMF中,易证FM=![]() ,HM=
,HM=![]() ,
,
∴HF=![]() =5.
=5.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?