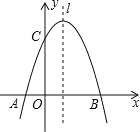
��Ŀ����
����Ŀ����ͼ�����������Ľ����������ߺͳ����ι��ɣ������εij�OAΪ12cm����OBΪ4cm����������D��·��ľ���Ϊ10cm��������ͼ��ʾ��ֱ������ϵ
��1����������ߵĽ���ʽ��
��2��һ������������һ�����弯װ�䣬��װ����ߴ���������Ϊ6m����Ϊ4m����������˫���г����������������ܷ�ȫͨ����
��3������������������Ҫ��װ���ŵƣ�ʹ���������߶���ȣ�����������ĸ߶Ȳ�����8.5m����ô���ŵƵ�ˮƽ������С�Ƕ����ף�
���𰸡�(1) y=![]() +10��(2)�ܰ�ȫͨ����(3) 6�ף�
+10��(2)�ܰ�ȫͨ����(3) 6�ף�
��������
�����������1����������ߵĽ���ʽ�����������߶������꣬�������ʽ��
��2����x=10�����y��6���Ƚϣ�
��3�����y=8.5ʱx��ֵ���ɵã�
�����������1���������⣬�������ߵĶ�������Ϊ��6��10����
�������߽���ʽΪ��y=![]() +10��
+10��
����B��0��4�����룬�ã�36a+10=4��
��ã�a=![]() ��
��
�ʸ������߽���ʽΪy=![]() +10��
+10��
��2���������⣬��x=6+4=10ʱ��y=![]() ��16+10=
��16+10=![]() ��6��
��6��
�����������ܰ�ȫͨ����
��3����y=8.5ʱ���У�![]() +10=8.5��
+10=8.5��
��ã�![]() =3��
=3��![]() =9��
=9��
��![]() ��
��![]() =6��
=6��
�����ŵƵ�ˮƽ������С��6�ף�

����Ŀ��С��ˮƽ��һ��ָ�������˾�����1000��Ԫ.2008���ij�ؽ�������������飬�ó�10�����˾����룬�����˾�1000��Ԫ����Ϊ�ﵽС��ָ�꣬����1000��Ԫ����Ԫ����������ʾ������1000��Ԫ����Ԫ���ø�����ʾ����10�������˾��������£���λ����Ԫ����
+500 | -300 | +200 | 0 | +1000 | -100 | +400 | -200 | +100 | +100 |
��1��������һ����10���аٷ�֮���ٴﵽ��С��ָ�ꣿ
��2��10����ƽ������Ϊ������Ԫ��