题目内容
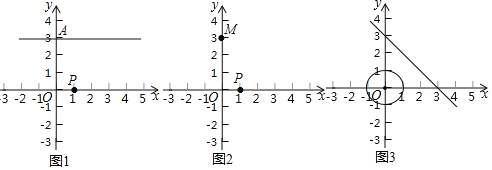
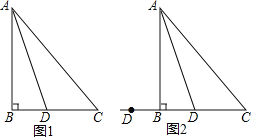
【题目】已知:如图,点A,B,C三点在⊙O上,AE平分∠BAC,交⊙O于点E,交BC于点D,过点E作直线l∥BC,连结BE.
(1)求证:直线l是⊙O的切线;
(2)如果DE=a,AE=b,写出求BE的长的思路.

【答案】(1)证明见解析;(2)见解析.
【解析】
(1)作辅助线,连接半径,由角平分线得:∠BAE=∠CAE,圆周角相等,则弧相等,再由垂径定理证明OE⊥BC,所以OE⊥l,直线l与⊙O相切;
(2)根据∠BAE=∠CAE、∠CAE=∠CBE结合公共角证△ABE∽△BDE可得![]() ,从而得出答案.
,从而得出答案.
解: (1)如图,连接OE、OB、OC,
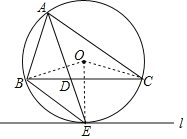
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴![]() ,
,
∴∠BOE=∠COE,
∵OB=OC,
∴OE⊥BC,
∵l∥BC,
∴OE⊥l,
∴直线l是⊙O的切线;
(2)∵∠BAE=∠CAE,∠CAE=∠CBE,
∴∠BAE=∠DBE,
又∵∠AEB=∠BED,
∴△ABE∽△BDE,
∴![]() ,
,
∴BE2=AEDE=ab.

【题目】2022年将在北京﹣﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 | 队员1 | 队员1 | 队员1 | 队员1 | 队员1 | |
甲组 | 176 | 177 | 175 | 176 | 177 | 175 |
乙组 | 178 | 175 | 170 | 174 | 183 | 176 |
设两队队员身高的平均数依次为![]() ,
,![]() ,方差依次为
,方差依次为![]() ,
,![]() ,下列关系中正确的是( )
,下列关系中正确的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,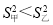 D.
D.![]() ,
,![]()
【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间 | 平均数 | 中位数 | 众数 |
甲车间 | 178 | m | 183 |
乙车间 | 177 | 182 | 184 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.