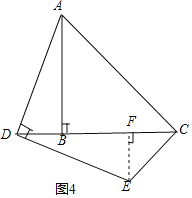
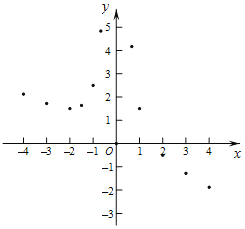ЬтФПФкШн
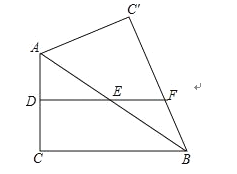
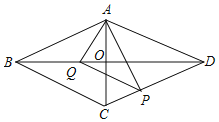
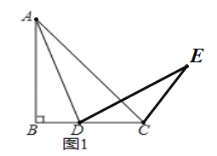
ЁОЬтФПЁПдкЁїABCжаЃЌABЃНBCЃЌЁЯBЃН90ЁуЃЌЕуDЮЊжБЯпBCЩЯЕФвЛИіЖЏЕу(ВЛгыBЁЂCжиКЯ)ЃЌСЌНсADЃЌНЋЯпЖЮADШЦЕуDАДЫГЪБеыЗНЯђа§зЊ90ЁуЃЌЪЙЕуAа§зЊЕНЕуEЃЌСЌНсECЃЎ
(1)ШчЙћЕуDдкЯпЖЮBCЩЯдЫЖЏЃЌШчЭМ1ЃК
ЂйвРЬтвтВЙШЋЭМ1ЃЛ
ЂкЧѓжЄЃКЁЯBADЃНЁЯEDCЃЛ
ЂлЭЈЙ§ЙлВьЁЂЪЕбщЃЌаЁУїЕУГіНсТлЃКдкЕуDдЫЖЏЕФЙ§ГЬжаЃЌзмгаЁЯDCEЃН135ЁуЃЌЃЎ
аЁУїгыЭЌбЇЬжТлКѓЃЌаЮГЩСЫжЄУїетИіНсТлЕФМИжжЯыЗЈЃК
ЯыЗЈвЛЃКдкABЩЯШЁвЛЕуFЃЌЪЙЕУBFЃНBDЃЌвЊжЄЁЯDCEЃН135ЁуЃЌжЛашжЄЁїADFЁеЁїDECЃЎ
ЯыЗЈЖўЃКвдЕуDЮЊдВаФЃЌDCЮЊАыОЖЛЛЁНЛACгкЕуFЃЌвЊжЄЁЯDCEЃН135ЁуЃЌжЛашжЄЁїAFDЁеЁїDCEЃЎ
ЯыЗЈШ§ЃКЙ§ЕуEзїBCЫљдкжБЯпЕФДЙжБЯпЖЮEFЃЌвЊжЄЁЯDCEЃН135ЁуЃЌжЛашжЄEFЃНCFЃЎ
ЧыФуВЮПМЩЯУцЕФЯыЗЈЃЌжЄУїЁЯDCEЃН135Ёу
(2)ШчЙћЕуDдкЯпЖЮCBЕФбгГЄЯпЩЯдЫЖЏЃЌРћгУЭМ2ЛЭМЗжЮіЃЌЁЯDCEЕФЖШЪ§ЛЙЪЧШЗЖЈЕФжЕТ№ЃПШчЙћЪЧЃЌжБНгаДГіЁЯDCEЕФЖШЪ§ЃЛШчЙћВЛЪЧЃЌЫЕУїРэгЩЃЎ
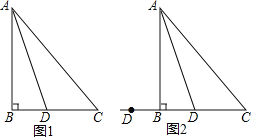
ЁОД№АИЁП(1)ЂйМћНтЮіЃЛЂкжЄУїМћНтЮіЃЛЂлжЄУїМћНтЮіЃЛ(2)ЁЯDCEЃН45Ёу.
ЁОНтЮіЁП
(1)ЂйИљОнЬтвтзїГіЭМаЮМДПЩЃЛЂкИљОнгрНЧЕФаджЪЕУЕННсТлЃЛЂлжЄЗЈ1ЃКдкABЩЯШЁЕуFЃЌЪЙЕУBFЃНBDЃЌСЌНгDFЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕНЁЯBFDЃН45ЁуЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯDCEЃНЁЯAFDЃН135ЁуЃЛжЄЗЈ2ЃКвдDЮЊдВаФЃЌDCЮЊАыОЖзїЛЁНЛACгкЕуFЃЌСЌНгDFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛжЄЗЈ3ЃКЙ§ЕуEзїEFЁЭBCНЛBCЕФбгГЄЯпгкЕуFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
(2)Й§EзїEFЁЭDCгкFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНDBЃНEFЃЌABЃНDFЃНBCЃЌИљОнЯпЖЮЕФКЭВюЕУЕНFCЃНEFЃЌгкЪЧЕУЕННсТлЃЎ
НтЃК(1)ЂйШчЭМЂйЫљЪОЃЛ
ЂкжЄУїЃКЁпЁЯBЃН90ЁуЃЌ
ЁрЁЯBAD+ЁЯBDAЃН90ЁуЃЌ
ЁпЁЯADEЃН90ЁуЃЌЕуDдкЯпЖЮBCЩЯЃЌ
ЁрЁЯBAD+ЁЯEDCЃН90ЁуЃЌ
ЁрЁЯBADЃНЁЯEDCЃЛ
ЂкжЄЗЈ1ЃКШчЭМЃЌдкABЩЯШЁЕуFЃЌЪЙЕУBFЃНBDЃЌСЌНгDFЃЌ
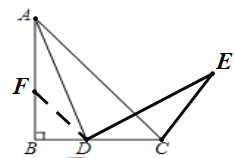
ЁпBFЃНBDЃЌЁЯBЃН90ЁуЃЌ
ЁрЁЯBFDЃН45ЁуЃЌ
ЁрЁЯAFDЃН135ЁуЃЌ
ЁпBAЃНBCЃЌ
ЁрAFЃНCDЃЌ
дкЁїADFКЭЁїDECжаЃЌ
ЁрЁїADFЁеЁїDECЃЌ
ЁрЁЯDCEЃНЁЯAFDЃН135ЁуЃЛ
жЄЗЈ2ЃКвдDЮЊдВаФЃЌDCЮЊАыОЖзїЛЁНЛACгкЕуFЃЌСЌНгDFЃЌ
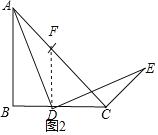
ЁрDCЃНDFЃЌЁЯDFCЃНЁЯDCFЃЌ
ЁпЁЯBЃН90ЁуЃЌABЃНBCЃЌ
ЁрЁЯACBЃН45ЁуЃЌЁЯDFCЃН45ЁуЃЌ
ЁрЁЯDFCЃН90ЁуЃЌЁЯAFDЃН135ЁуЃЌ
ЁпЁЯADEЃНЁЯFDCЃН90ЁуЃЌ
ЁрЁЯADFЃНЁЯEDCЃЌ
дкЁїADFЁеЁїCDEжаЃЌ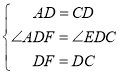 ЃЌ
ЃЌ
ЁрЁїADFЁеЁїCDEЃЌ
ЁрЁЯAFDЃНЁЯDCEЃН135ЁуЃЛ
жЄЗЈ3ЃКЙ§ЕуEзїEFЁЭBCНЛBCЕФбгГЄЯпгкЕуFЃЌ
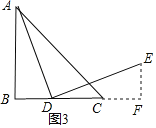
ЁрЁЯEFDЃН90ЁуЃЌ
ЁпЁЯBЃН90ЁуЃЌ
ЁрЁЯEFDЃНЁЯBЃЌ
дкЁїABDКЭЁїDFEжаЃЌ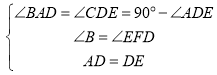 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїDFEЃЌ
ЁрABЃНDFЃЌBDЃНEFЃЌ
ЁпABЃНBCЃЌ
ЁрBCЃНDFЃЌBCЉDCЃНDFЉDCЃЌ
МДBDЃНCFЃЌ
ЁрEFЃНCFЃЌ
ЁпЁЯEFCЃН90ЁуЃЌ
ЁрЁЯECFЃН45ЁуЃЌЁЯDCEЃН135ЁуЃЛ
(2)НтЃКЁЯDCEЃН45ЁуЃЌ
РэгЩЃКЙ§EзїEFЁЭDCгкFЃЌ
ЁпЁЯABDЃН90ЁуЃЌ
ЁрЁЯEDFЃНЁЯDABЃН90ЁуЉЁЯADBЃЌ
дкЁїABDКЭЁїDFEжаЃЌ ЃЌ
ЃЌ
ЁрЁїABDЁеЁїDFEЃЌ
ЁрDBЃНEFЃЌABЃНDFЃНBCЃЌ
ЁрBCЉBFЃНDFЉBFЃЌ
МДFCЃНDBЃЌ
ЁрFCЃНEFЃЌ
ЁрЁЯDCEЃН45ЁуЃЎ

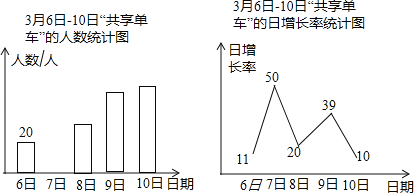
ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПКЏЪ§![]() ЕФЭМЯѓгыаджЪЃЎ
ЕФЭМЯѓгыаджЪЃЎ
аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃЌВЂНтОіЯрЙиЮЪЬтЃК
ЃЈ1ЃЉКЏЪ§![]() ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ2ЃЉЯТБэЪЧyгыxЕФМИзщЖдгІжЕЃЌЧѓmЕФжЕЃЛ
x | Ё |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | Ё |
y | Ё |
|
|
|
|
|
|
|
|
|
| m | Ё |
ЃЈ3ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЎИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉНјвЛВНЬНОПЗЂЯжЃЌИУКЏЪ§ЭМЯѓдкЕкЖўЯѓЯоФкЕФзюЕЭЕуЕФзјБъЪЧ![]() ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФЦфЫќаджЪЃЈвЛЬѕМДПЩЃЉ ЃЎ
ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФЦфЫќаджЪЃЈвЛЬѕМДПЩЃЉ ЃЎ
ЃЈ5ЃЉИљОнКЏЪ§ЭМЯѓЙРЫуЗНГЬ![]() ЕФИљЮЊ ЃЎЃЈОЋШЗЕН0.1ЃЉ
ЕФИљЮЊ ЃЎЃЈОЋШЗЕН0.1ЃЉ