Question

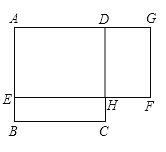
【题目】如图，ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形AEFG的形状，其中点E在AB边上，点G在AD的延长线上，DG= 2BE．设BE的长为x米，改造后苗圃AEFG的面积为y平方米．

（1）求y与x之间的函数关系式（不需写自变量的取值范围）；

（2）根据改造方案，改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？

Answer 1

【答案】（1）y=-2x+4x+16；（2）2米

【解析】

（1）若BE的长为x米，则改造后矩形的宽为米，长为米，求矩形面积即可得出y与x之间的函数关系式；

（2）根据题意可令函数值为16，解一元二次方程即可．

解：（1）∵BE边长为x米，

∴AE=AB-BE=4-x，AG=AD+DG=4+2x

苗圃的面积=AE×AG=(4-x)(4+2x)

则苗圃的面积y（单位：米2）与x（单位：米）的函数关系式为：y=-2x+4x+16

（2）依题意，令y=16 即-2x+4x+16=16

解得：x=0(舍）x=2

答：此时BE的长为2米．