��Ŀ����
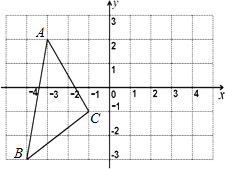
����Ŀ�� ��2016����ͼ1��һ�κ���y=kx��3��k��0����ͼ����y�ύ�ڵ�A���뷴��������![]() ��x��0����ͼ���ڵ�B��4��b����
��x��0����ͼ���ڵ�B��4��b����
��1��b= ��k= ��
��2����C���߶�AB�ϵĶ��㣨�ڵ�A��B���غϣ�������C��ƽ����y���ֱ��l�����������������ͼ���ڵ�D������OCD��������ֵ��
��3������2�������ȡ�����ֵ����OCD������AB����ƽ��һ���ľ��룬�õ���O��C��D�䣬����O�Ķ�Ӧ��O�����ڸ÷���������ͼ���ϣ���ͼ2�������D��������� ��

���𰸡���1��1��1����2��![]() ����3��D�䣨
����3��D�䣨![]() ��
��![]() ����
����
��������
�����������1���ɵ�B�ĺ��������÷���������ͼ���ϵ�����������������bֵ�������ó���B�����꣬�ٽ���B���������һ�κ�������ʽ�м������kֵ��
��2����C��m��m��3����0��m��4������D��m��![]() �������������ε�������ɵó�S��OCD����m�ĺ�����ϵʽ��ͨ���䷽���ɵó���OCD��������ֵ��
�������������ε�������ɵó�S��OCD����m�ĺ�����ϵʽ��ͨ���䷽���ɵó���OCD��������ֵ��
��3���ɣ�1����2����֪һ�κ����Ľ���ʽ�Լ���C��D�����꣬���C�䣨a��a��3��������ƽ�Ƶ������ҳ���O�䡢D������꣬�ɵ�O���ڷ���������ͼ���ϼ��ɵó�����a�ķ��̣��ⷽ�����a��ֵ����������D��������м��ɵó����ۣ�
�����������1����B��4��b������![]() ��x��0���еã�b=
��x��0���еã�b=![]() =1����B��4��1������B��4��1������y=kx��3�ã�1=4k��3����ã�k=1���ʴ�Ϊ��1��1��
=1����B��4��1������B��4��1������y=kx��3�ã�1=4k��3����ã�k=1���ʴ�Ϊ��1��1��
��2����C��m��m��3����0��m��4������D��m��![]() ������S��OCD=
������S��OCD=![]() =
=![]() =
=![]() ����0��m��4��
����0��m��4��![]() ��0������m=
��0������m=![]() ʱ����OCD���ȡ���ֵ�����ֵΪ
ʱ����OCD���ȡ���ֵ�����ֵΪ![]() ��
��
��3���ɣ�1��֪һ�κ����Ľ���ʽΪy=x��3���ɣ�2��֪C��![]() ����
����![]() ����D��
����D��![]() ��
��![]() ����
����
��C�䣨a��a��3������O�䣨a��![]() ��a��
��a��![]() ����D�䣨a��a+
����D�䣨a��a+![]() ��������O���ڷ���������
��������O���ڷ���������![]() ��x��0����ͼ���ϣ���
��x��0����ͼ���ϣ��� ����ã�a=
����ã�a=![]() ��a=��
��a=��![]() ����ȥ����������a=
����ȥ����������a=![]() �Ƿ���
�Ƿ��� �Ľ⣬����D��������ǣ�
�Ľ⣬����D��������ǣ�![]() ��
��![]() ����
����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�