题目内容
(2012•乐山模拟)选做题
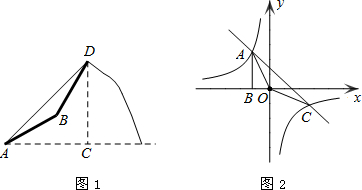
甲题:如图1,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD.(结果保留根号)
乙题:如图2,Rt△ABO的顶点A是双曲线y=
与直线y′=-x-(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO=
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标,并写出当x在什么范围取值时,y′≥y.
甲题:如图1,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD.(结果保留根号)
乙题:如图2,Rt△ABO的顶点A是双曲线y=
| k |
| x |
| 3 |
| 2 |
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标,并写出当x在什么范围取值时,y′≥y.

分析:甲题:首先根据题意分析图形;过点B作CD,AC的垂线,垂足分别为E,F,构造两个直角三角形△ABE与△BDF,分别求解可得DF与EB的值,再利用图形关系,进而可求出答案;
乙题:(1)先根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)直接根据一次函数与反比例函数的交点坐标求出一次函数的值大于反比例函数的值x的取值范围即可.
乙题:(1)先根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)直接根据一次函数与反比例函数的交点坐标求出一次函数的值大于反比例函数的值x的取值范围即可.
解答:甲题: 解:如图1,过点B作CD,AC的垂线,垂足分别为E,F,
解:如图1,过点B作CD,AC的垂线,垂足分别为E,F,
∵∠BAC=30°,AB=1500米,
∴BF=EC=750米.
AF=AB•cos∠BAC=1500×
=750
米.
设FC=x米,
∵∠DBE=60°,
∴DE=
x米.
又∵∠DAC=45°,
∴AC=CD.
即:750
+x=750+
x,
解得x=750.
则CD=750(
+1)米.
答:山高CD为750(
+1)米.
乙题:解:(1)设A点坐标为(x,y)且x<0,y>0,
则S△AB0=
|BO||BA|=
(-x)y=
,
∴xy=-3,
又∵y=kx,xy=k,
∴k=-3,
∴所求的两个函数的解析式分别为y=-
,y=-x+2;
(2)∵A(-1,3),C(3,-1),
∴当x≤-1或0<x≤3时,一次函数的值小于反比例函数的值,即y'≥y.
 解:如图1,过点B作CD,AC的垂线,垂足分别为E,F,
解:如图1,过点B作CD,AC的垂线,垂足分别为E,F,∵∠BAC=30°,AB=1500米,
∴BF=EC=750米.
AF=AB•cos∠BAC=1500×
| ||
| 2 |
| 3 |
设FC=x米,
∵∠DBE=60°,
∴DE=
| 3 |
又∵∠DAC=45°,
∴AC=CD.
即:750
| 3 |
| 3 |
解得x=750.
则CD=750(
| 3 |
答:山高CD为750(
| 3 |
乙题:解:(1)设A点坐标为(x,y)且x<0,y>0,
则S△AB0=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴xy=-3,
又∵y=kx,xy=k,
∴k=-3,
∴所求的两个函数的解析式分别为y=-
| 3 |
| x |
(2)∵A(-1,3),C(3,-1),
∴当x≤-1或0<x≤3时,一次函数的值小于反比例函数的值,即y'≥y.
点评:本题考查了反比例函数与一次函数的交点问题和俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形以及能根据△ABO的面积求出k的值是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
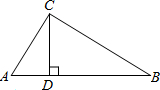 (2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )
(2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )