题目内容
阅读:我们知道,在数轴上x=1表示一个点,而平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图①.观察图①可以得出:直线x=1与直线y=2x+1的交P的坐标(1,3)就是方程组
的解,所以这个方程组的解是
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它的右下方的部分,如图③.
回答下列问题:
(1)在直角坐标系(图④)中,用作图象的方法求出方程组
的解;
(2)用阴影部分表示不等式组
所围成的平面区域,并求围成区域的面积;
(3)现有一直角三角形(其中∠A=90°,AB=2,AC=4)小车沿x轴自左向 右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?
右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?
|
|
回答下列问题:
(1)在直角坐标系(图④)中,用作图象的方法求出方程组
|
(2)用阴影部分表示不等式组
|
(3)现有一直角三角形(其中∠A=90°,AB=2,AC=4)小车沿x轴自左向
 右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?
右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?(1)如图,由图象可得方程组的解是
;
(2)不等式组
所围成的平面区域如图所示;
阴影部分的面积是
×6×3=9;
(3)由题意,BC所在直线与二元一次方程2x+y-2=0所表示的直线垂直.
设小车沿x轴自左向右运动,当点A的坐标为(a,0)时,小车被阴影部分挡住的面积最大.分五种情况:
①当-2≤a≤0时,此时点A与原点重合时,小车被挡住的面积最大为
=3;
②当0≤a≤1时,此时被挡住的面积为:
S=
•
•
-
-
=
-(a-1)2-
=
,
∴当a=
时Smax=
;
③当1≤a≤2时,此时被挡住的面积为:
S=
•
-
-
=
-
=
,
∴当a=1时Smax=
;
④当2≤a≤5时,此时点A与点(2,0)重合时,小车被挡住的面积最大为
;
⑤当a<-2或a>5时,小车与阴影无公共部分.
综上所述,当点A的坐标为(
,0)时,小车被挡住的面积最大为
.(12分)

|
(2)不等式组
|
阴影部分的面积是
| 1 |
| 2 |
(3)由题意,BC所在直线与二元一次方程2x+y-2=0所表示的直线垂直.
设小车沿x轴自左向右运动,当点A的坐标为(a,0)时,小车被阴影部分挡住的面积最大.分五种情况:
①当-2≤a≤0时,此时点A与原点重合时,小车被挡住的面积最大为
| (1+2)×2 |
| 2 |
②当0≤a≤1时,此时被挡住的面积为:
S=
| 1 |
| 2 |
| 10-2a | ||
|
| 10-2a | ||
2
|
| 2(1-a)(1-a) |
| 2 |
| (a-2)2 |
| 4 |
| (a-5)2 |
| 5 |
| (a-2)2 |
| 4 |
| -21a2+20a+60 |
| 20 |
∴当a=
| 10 |
| 21 |
| 68 |
| 21 |
③当1≤a≤2时,此时被挡住的面积为:
S=
| 1 |
| 2 |
| 10-2a | ||
|
| 10-2a | ||
2
|
| (a-2)2 |
| 4 |
| (a-5)2 |
| 5 |
| (a-2)2 |
| 4 |
| -a2-20a+80 |
| 20 |
∴当a=1时Smax=
| 59 |
| 20 |
④当2≤a≤5时,此时点A与点(2,0)重合时,小车被挡住的面积最大为
| 9 |
| 5 |
⑤当a<-2或a>5时,小车与阴影无公共部分.
综上所述,当点A的坐标为(
| 10 |
| 21 |
| 68 |
| 21 |


练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
 在第二象限的图象如图所示.
在第二象限的图象如图所示. 的图象与上述反比例函数图象交于点A,与x轴交于点B,△AOB的面积为
的图象与上述反比例函数图象交于点A,与x轴交于点B,△AOB的面积为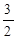 ,求m的值.
,求m的值.





 千克,付款金额
千克,付款金额 为元,则
为元,则