题目内容
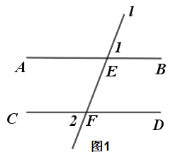
【题目】已知：直线l分别交AB、CD与E、F两点，且AB∥CD．
（1） 说明：∠1=∠2；
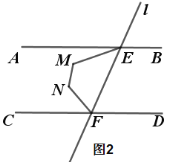
（2） 如图2，点M、N在AB、CD之间，且在直线l左侧，若∠EMN+∠FNM=260°，
①求：∠AEM+∠CFN的度数；
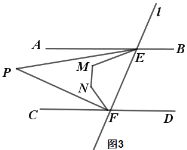
②如图3，若EP平分∠AEM，FP平分∠CFN，求∠P的度数；
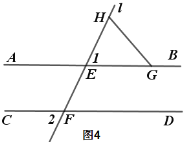
（3） 如图4，∠2=80°，点G在射线EB上，点H在AB上方的直线l上，点Q是平面内一点，连接QG、QH，若∠AGQ=18°，∠FHQ=24°，直接写出∠GQH的度数．
【答案】（1）理由见解析；（2）①80°，②40°；（3）38°、74°、86°、122°．
【解析】
（1）根据平行线的性质及对顶角的性质即可得证；
（2）①过拐点作AB的平行线，根据平行线的性质推理即可得到答案；
②过点P作AB的平行线，根据平行线的性质及角平分线的定义求得角的度数；
（3）分情况讨论，画出图形，根据三角形的内角和与外角的性质分别求出答案即可．
（1）
，
；
（2）①分别过点M，N作直线GH，IJ与AB平行，则
，如图：
，
，
，
；
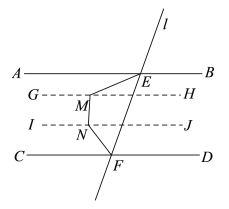
②过点P作AB的平行线，
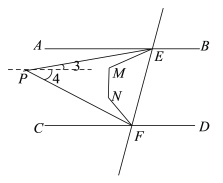
根据平行线的性质可得：
，
，
∵EP平分∠AEM，FP平分∠CFN，
∴
，
即
；
（3）分四种情况进行讨论：
由已知条件可得
，
①如图：
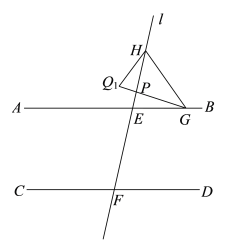
②如图：
，
；
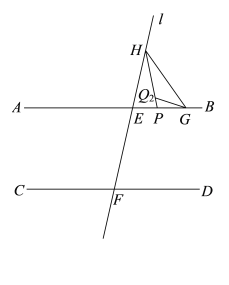
③如图：
，
；
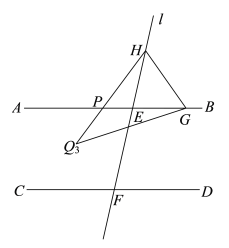
④如图：
，
；
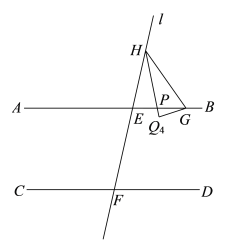
综上所述，∠GQH的度数为38°、74°、86°、122°．
练习册系列答案
互动课堂系列答案
相关题目
