题目内容
【题目】用两种方法证明“四边形的外角和等于360°”.
如图,∠DAE、∠ABF、∠BCG、∠CDH是四边形ABCD的四个外角.
求证:∠DAE+∠ABF+∠BCG+∠CDH=360°.

【答案】详见解析.
【解析】
连接AC,BD,由三角形外角和可知∠EAD=∠ABD+∠ADB,∠ABF=∠CAB+∠ACB,∠BCG=∠CDB+∠CBD,∠CDH=∠DAC+∠DCA,代入所求式子即可求解.
解:解法一:连接AC,BD,
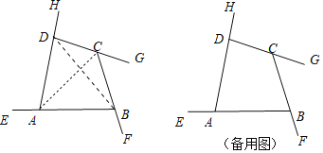
∵∠EAD=∠ABD+∠ADB,
∠ABF=∠CAB+∠ACB,
∠BCG=∠CDB+∠CBD,
∠CDH=∠DAC+∠DCA,
∴∠DAE+∠ABF+∠BCG+∠CDH=∠ACB+∠ABC+∠CAB+∠ACB+∠CDB+∠CBD+∠DAC+∠DCA=(∠ACD+∠DCA+∠ADC)+(∠ABC+∠DAB+∠ACB)=180°+180°=360°.
解法二:
∵∠DAE+∠ABF+∠BCG+∠CDH=180°∠DAB+180°∠ABC+180°∠BCD+180°∠ADC,
又∵∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠DAE+∠ABF+∠BCG+∠CDH=360°.
【解答】
本题考查三角形的外角和和内角和定理;通过辅助线将四边形分割成三角形,在三角形中求解是关键.

练习册系列答案
相关题目